题目内容
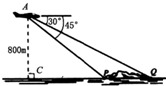 某次飞行表演中,一架直升从空中A处测出前下方海岛两侧海岸P、Q处的俯角分别是45°和30°(如右图所示,A、P、Q在同一平面内).
某次飞行表演中,一架直升从空中A处测出前下方海岛两侧海岸P、Q处的俯角分别是45°和30°(如右图所示,A、P、Q在同一平面内).(1)若直升飞机在海拔800m的高度飞行,试计算这个海岛的宽度PQ.
(2)若地面观测者测得P、Q两海岸距离大约为600m,由此试估算出观测者甲(在P处)到飞机的直线距离(精确到100m).
考点:解三角形的实际应用
专题:综合题,解三角形
分析:(1)先在Rt△ACP中求出PC,再在Rt△ACQ中求出CQ,即可求出这个海岛的宽度PQ.
(2)先在△APQ中锝,PQ=600,∠AQP=30°,∠PAQ=45°-30°=15°.再利用正弦定理即可求出PA,即为观测者甲(在P处)到飞机的直线距离.
(2)先在△APQ中锝,PQ=600,∠AQP=30°,∠PAQ=45°-30°=15°.再利用正弦定理即可求出PA,即为观测者甲(在P处)到飞机的直线距离.
解答:
解:(1)在Rt△ACP中,
=tan∠CAP,
则PC=800×tan45°=800.(3分)
在Rt△ACQ中,
=tan∠CAQ,则QC=800
.(5分)
所以,PQ=QC-PC=800
-800(m).(7分)
(2)在△APQ中,PQ=600,∠AQP=30°,∠PAQ=45°-30°=15°.(8分)
根据正弦定理,得
=
,(10分)
则PA=300(
+
)≈11589m.
故观测者甲(在P处)到飞机的直线距离为11589m(14分)
| PC |
| AC |
则PC=800×tan45°=800.(3分)
在Rt△ACQ中,
| QC |
| AC |
| 3 |
所以,PQ=QC-PC=800
| 3 |
(2)在△APQ中,PQ=600,∠AQP=30°,∠PAQ=45°-30°=15°.(8分)
根据正弦定理,得
| PA |
| sin30° |
| 600 |
| sin15° |
则PA=300(
| 6 |
| 2 |
故观测者甲(在P处)到飞机的直线距离为11589m(14分)
点评:本题主要考查解三角形的实际应用.这一类型题目,一般都是借助与正弦定理,余弦定理来求解.

练习册系列答案
 出彩同步大试卷系列答案
出彩同步大试卷系列答案
相关题目
钱大姐常说“好货不便宜”,她这句话的意思是:“好货”是“不便宜”的( )
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充分必要条件 |
| D、既非充分又非必要条件 |
已知椭圆
+
=1(a>b>0),F为左焦点,A为左顶点,B为上顶点,C为下顶点,且
•
=0,则椭圆的离心率为( )
| x2 |
| a2 |
| y2 |
| b2 |
| AB |
| CF |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
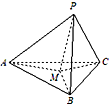 如图,在三棱锥P-ABC中,PA、PB、PC两两垂直,且PA=3,PB=2,PC=2.设M是底面ABC内一点,定义f(M)=(m,n,p),其中m、n、p分别是三棱锥M-PAB、三棱锥M-PBC、三棱锥M-PCA的体积.若f(M)=(
如图,在三棱锥P-ABC中,PA、PB、PC两两垂直,且PA=3,PB=2,PC=2.设M是底面ABC内一点,定义f(M)=(m,n,p),其中m、n、p分别是三棱锥M-PAB、三棱锥M-PBC、三棱锥M-PCA的体积.若f(M)=(