题目内容
已知F1、F2为椭圆C:
+
=1(a>b>0)的左右焦点,椭圆C的离心率为
,过左焦点F1的直线与C相交于A、B两点,△ABF2面积的最大值为3
,求椭圆C的方程.
| x2 |
| a2 |
| y2 |
| b2 |
| ||
| 2 |
| 2 |
考点:椭圆的简单性质
专题:圆锥曲线的定义、性质与方程
分析:当AB与椭圆的长轴垂直时,△ABF2面积取最大值,此时|AB|=
,AB边上的高为2c,结合椭圆C的离心率e=
=
和a2=b2+c2,可得椭圆C的方程.
| 2b2 |
| a |
| c |
| a |
| ||
| 2 |
解答:
解:当AB与椭圆的长轴垂直时,△ABF2面积取最大值,
此时|AB|=
,
AB边上的高为2c,
∵此时△ABF2面积为3
,
故
×
×2c=3
,
又∵椭圆C的离心率e=
=
,
又由a2=b2+c2,
解得:a2=6,b2=3,
故椭圆C的方程为:
+
=1.
此时|AB|=
| 2b2 |
| a |
AB边上的高为2c,
∵此时△ABF2面积为3
| 2 |
故
| 1 |
| 2 |
| 2b2 |
| a |
| 2 |
又∵椭圆C的离心率e=
| c |
| a |
| ||
| 2 |
又由a2=b2+c2,
解得:a2=6,b2=3,
故椭圆C的方程为:
| x2 |
| 6 |
| y2 |
| 3 |
点评:本题考查的知识点是椭圆的简单性质,由已知构造方程,求出a2=6,b2=3,是解答的关键.

练习册系列答案
 直通贵州名校周测月考直通名校系列答案
直通贵州名校周测月考直通名校系列答案
相关题目
在△ABC中,角A、B、C所对的边分别为a、b、c,若a•cosA=bcosB,则△ABC的形状为( )
| A、等腰三角形 |
| B、直角三角形 |
| C、等腰三角形或直角三角形 |
| D、等腰直角三角形 |
已知圆(x-3)2+(y-4)2=4和直线y=x相交于P,Q两点则|OP|•|OQ|的值是( )
A、
| ||
| B、2 | ||
| C、4 | ||
| D、21 |
用二分法求函数f(x)=ex-4x+1在区间(1,2)内零点的近似值的过程中得到f(15)<0,f(1.75)<0,f(1.875)>0,f(2)>0则函数零点落在区间( )
| A、(1.5,1.75) |
| B、(1.75,1.875) |
| C、(1.875,2) |
| D、不能确定 |
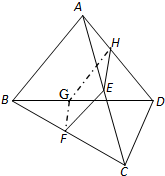 如图,在四面体ABCD中,平行于AB,CD的平面β截四面体所得截面为EFGH.
如图,在四面体ABCD中,平行于AB,CD的平面β截四面体所得截面为EFGH.