题目内容
双曲线与椭圆
+y2=1有相同的焦点F1、F2,P在双曲线的右支上,且PF2⊥F1F2,∠PF1F2=30°,则双曲线的方程是 .
| x2 |
| 4 |
考点:双曲线的简单性质,椭圆的简单性质
专题:计算题,圆锥曲线的定义、性质与方程
分析:由椭圆方程可得双曲线的c=
,设双曲线方程为:
-
=1.又PF2⊥F1F2,则令x=c,求得y=
,即PF2=
,再由∠PF1F2=30°,则PF2=tan30°F1F2,即可得到a,b的方程,再由a2+b2=3,即可解得a,b,进而得到双曲线方程.
| 3 |
| x2 |
| a2 |
| y2 |
| b2 |
| b2 |
| a |
| b2 |
| a |
解答:
解:椭圆
+y2=1的焦点F1(-
,0),F2(
,0),
则双曲线的c=
,设双曲线方程为:
-
=1.
又PF2⊥F1F2,则令x=c,求得y=
,即PF2=
,
再由∠PF1F2=30°,则PF2=tan30°F1F2,
即有
=
•2c=2,且a2+b2=3,
即可解得,a=1,b=
.
则双曲线方程为:x2-
=1.
故答案为:x2-
=1.
| x2 |
| 4 |
| 3 |
| 3 |
则双曲线的c=
| 3 |
| x2 |
| a2 |
| y2 |
| b2 |
又PF2⊥F1F2,则令x=c,求得y=
| b2 |
| a |
| b2 |
| a |
再由∠PF1F2=30°,则PF2=tan30°F1F2,
即有
| b2 |
| a |
| ||
| 3 |
即可解得,a=1,b=
| 2 |
则双曲线方程为:x2-
| y2 |
| 2 |
故答案为:x2-
| y2 |
| 2 |
点评:本题主要考查了椭圆、双曲线的简单性质,特别是双曲线方程的运用,属于基础题.

练习册系列答案
相关题目
数列{an}满足an+1+an=2n-3,若a1=2则a21-a20=( )
| A、9 | B、7 | C、5 | D、3 |
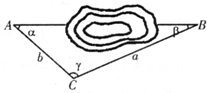 如图,为了测量隧道两口之间AB的长度,对给出的四组数据,求解计算时,较为简便易行的一组是( )
如图,为了测量隧道两口之间AB的长度,对给出的四组数据,求解计算时,较为简便易行的一组是( )| A、a,b,γ |
| B、a,b,α |
| C、a,b,β |
| D、α,β,a |
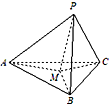 如图,在三棱锥P-ABC中,PA、PB、PC两两垂直,且PA=3,PB=2,PC=2.设M是底面ABC内一点,定义f(M)=(m,n,p),其中m、n、p分别是三棱锥M-PAB、三棱锥M-PBC、三棱锥M-PCA的体积.若f(M)=(
如图,在三棱锥P-ABC中,PA、PB、PC两两垂直,且PA=3,PB=2,PC=2.设M是底面ABC内一点,定义f(M)=(m,n,p),其中m、n、p分别是三棱锥M-PAB、三棱锥M-PBC、三棱锥M-PCA的体积.若f(M)=( 函数f(x)=Asin(ωx+ϕ)(A>0,ω>0|)的图象如下图所示,则f(1)+f(2)+f(3)+…+f(2014)=
函数f(x)=Asin(ωx+ϕ)(A>0,ω>0|)的图象如下图所示,则f(1)+f(2)+f(3)+…+f(2014)=