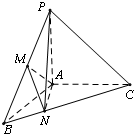
 如图,在三棱锥P-ABC中,PA⊥面ABC,∠BAC=120°,且AB=AC=AP,M为PB的中点,N在BC上,且BN=
如图,在三棱锥P-ABC中,PA⊥面ABC,∠BAC=120°,且AB=AC=AP,M为PB的中点,N在BC上,且BN=| 1 |
| 3 |
(1)求证:MN⊥AB;
(2)求平面MAN与平面PAN的夹角的余弦值.
设x≥4,则y=
的最小值是( )
| x2+x-5 |
| x-2 |
| A、7 | ||
| B、8 | ||
C、
| ||
| D、15 |
 如图,在三棱锥P-ABC中,PA⊥面ABC,∠BAC=120°,且AB=AC=AP,M为PB的中点,N在BC上,且BN=
如图,在三棱锥P-ABC中,PA⊥面ABC,∠BAC=120°,且AB=AC=AP,M为PB的中点,N在BC上,且BN=| 1 |
| 3 |
| x2+x-5 |
| x-2 |
| A、7 | ||
| B、8 | ||
C、
| ||
| D、15 |