题目内容
已知f(x)=-x+log2
.
(1)求f(
)+f(-
)的值;
(2)当x∈(-a,a](其中a∈(-1,1)且a为常数)时,f(x)是否存在最小值?如果存在,求函数最小值;若果不存在,请说明理由.
| 1-x |
| 1+x |
(1)求f(
| 1 |
| 2014 |
| 1 |
| 2014 |
(2)当x∈(-a,a](其中a∈(-1,1)且a为常数)时,f(x)是否存在最小值?如果存在,求函数最小值;若果不存在,请说明理由.
考点:函数最值的应用
专题:函数的性质及应用
分析:(1)利用函数的解析式代入数值求解即可.
(2)设-1<x1<x2<1,利用作差、因式分解、判断符号的方法,证出f(x)为(-1,1)上的减函数.因此,当a∈(0,1),且a为常数时,f(x)在区间(-a,a]的最小值为f(a)=-a+log2
.
(2)设-1<x1<x2<1,利用作差、因式分解、判断符号的方法,证出f(x)为(-1,1)上的减函数.因此,当a∈(0,1),且a为常数时,f(x)在区间(-a,a]的最小值为f(a)=-a+log2
| 1-a |
| 1+a |
解答:
解:(1)f(x)=-x+log2
.
f(
)+f(-
)=-
+log2
+
+log2
=log21=0.
(2)设-1<x1<x2<1,
∵f(x1)-f(x2)
=-x1+log2
-(-x2+log2
)
=(x2-x1)+log2
,
且x2-x1>0,
>1
∴log2
>0,
可得f(x1)-f(x2)>0,得f(x1)>f(x2),
由此可得f(x)为(-1,1)上的减函数,
∴当x∈(-a,a](其中a∈(0,1),且a为常数)时,
函数有最小值为f(a)=-a+log2
| 1-x |
| 1+x |
f(
| 1 |
| 2014 |
| 1 |
| 2014 |
| 1 |
| 2014 |
1-
| ||
1+
|
| 1 |
| 2014 |
1+
| ||
1-
|
(2)设-1<x1<x2<1,
∵f(x1)-f(x2)
=-x1+log2
| 1-x1 |
| 1+x1 |
| 1-x2 |
| 1+x2 |
=(x2-x1)+log2
| (1-x1)(1+x2) |
| (1+x1)(1-x2) |
且x2-x1>0,
| (1-x1)(1+x2) |
| (1+x1)(1-x2) |
∴log2
| (1-x1)(1+x2) |
| (1+x1)(1-x2) |
可得f(x1)-f(x2)>0,得f(x1)>f(x2),
由此可得f(x)为(-1,1)上的减函数,
∴当x∈(-a,a](其中a∈(0,1),且a为常数)时,
函数有最小值为f(a)=-a+log2
| 1-a |
| 1+a |
点评:本题给出含有对数符号的基本初等函数,求特殊的函数值并讨论函数在区间(-a,a]上的最小值,着重考查了函数的奇偶性、单调性及其应用的知识点,属于中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
下列命题正确的是( )
A、若向量
| ||||||||
B、若向量
| ||||||||
C、若向量
| ||||||||
D、若向量
|
 已知正方体ABCD-A1B1C1D1的棱长为2a,点E为棱CC1的中点.
已知正方体ABCD-A1B1C1D1的棱长为2a,点E为棱CC1的中点.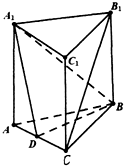 在直三棱柱中,AA1=AB=BC=3,AC=2,D是AC中点.
在直三棱柱中,AA1=AB=BC=3,AC=2,D是AC中点.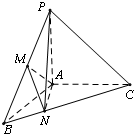 如图,在三棱锥P-ABC中,PA⊥面ABC,∠BAC=120°,且AB=AC=AP,M为PB的中点,N在BC上,且BN=
如图,在三棱锥P-ABC中,PA⊥面ABC,∠BAC=120°,且AB=AC=AP,M为PB的中点,N在BC上,且BN=