题目内容
已知函数f(x)=ex-e-x,其中e是自然对数的底数.
(1)证明:f(x)是R上的奇函数;
(2)若函数g(x)=e2x+e-2x-6f(x),求g(x)在区间[0,1]上的最大值.
(1)证明:f(x)是R上的奇函数;
(2)若函数g(x)=e2x+e-2x-6f(x),求g(x)在区间[0,1]上的最大值.
考点:利用导数求闭区间上函数的最值,函数奇偶性的判断,利用导数研究函数的单调性
专题:函数的性质及应用,导数的综合应用
分析:(1)由f(x)=ex-e-x,可得f(-x)=e-x-ex=-f(x),从而可得函数为奇函数;
(2)函数g(x)=e2x+e-2x-6f(x)=(ex-e-x)2+2-6f(x)=[f(x)]2-6f(x)+2,不妨令t=f(x),则g(x)=t2-6t+2,
先确定t的范围,求出原函数的最大值.
(2)函数g(x)=e2x+e-2x-6f(x)=(ex-e-x)2+2-6f(x)=[f(x)]2-6f(x)+2,不妨令t=f(x),则g(x)=t2-6t+2,
先确定t的范围,求出原函数的最大值.
解答:
(1)证明:函数f(x)的定义域为R,
∵f(x)=ex-e-x,
∴f(-x)=e-x-ex=-f(x),
∴函数f(x)为奇函数
(2)解:函数g(x)=e2x+e-2x-6f(x)=(ex-e-x)2+2-6f(x)=[f(x)]2-6f(x)+2,
不妨令t=f(x),则g(x)=t2-6t+2,易知g(x)在t∈(-∞,3)单调递减,
由f′(x)=ex+e-x>0可知f(x)在R上为单调递增函数,
所以f(x)在[0,1]上亦为单调递增函数,
从而t∈[f(0),f(1)]=[0,e-
]⊆(-∞,3),
所以g(x)的最大值在t=f(0)=0处取得,
即g(x)max=(0-3)2-7=2.
∵f(x)=ex-e-x,
∴f(-x)=e-x-ex=-f(x),
∴函数f(x)为奇函数
(2)解:函数g(x)=e2x+e-2x-6f(x)=(ex-e-x)2+2-6f(x)=[f(x)]2-6f(x)+2,
不妨令t=f(x),则g(x)=t2-6t+2,易知g(x)在t∈(-∞,3)单调递减,
由f′(x)=ex+e-x>0可知f(x)在R上为单调递增函数,
所以f(x)在[0,1]上亦为单调递增函数,
从而t∈[f(0),f(1)]=[0,e-
| 1 |
| e |
所以g(x)的最大值在t=f(0)=0处取得,
即g(x)max=(0-3)2-7=2.
点评:本题考查利用导数研究函数的单调性、函数在闭区间上的最值、二次不等式的求解,考查学生解决问题的能力,属中档题.

练习册系列答案
相关题目
设f(x)=|xex|,若关于x的方程(1-t)f2(x)-f(x)+t=0有四个不同的实数根,则实数t的取值范围为( )
| A、(-∞,0) | ||
B、(0,
| ||
C、(
| ||
| D、(1,+∞) |
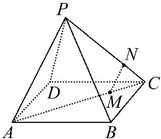 如图,四棱锥P-ABCD中,M,N分别为AC,PC上的点,且MN∥平面PAD,则( )
如图,四棱锥P-ABCD中,M,N分别为AC,PC上的点,且MN∥平面PAD,则( )| A、MN∥PD |
| B、MN∥PA |
| C、MN∥AD |
| D、以上均有可能 |
函数f(x)=sinx+cos2x的图象为( )
A、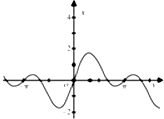 |
B、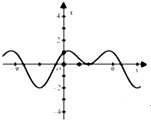 |
C、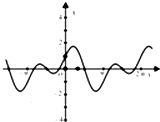 |
D、 |
