题目内容
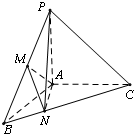 如图,在三棱锥P-ABC中,PA⊥面ABC,∠BAC=120°,且AB=AC=AP,M为PB的中点,N在BC上,且BN=
如图,在三棱锥P-ABC中,PA⊥面ABC,∠BAC=120°,且AB=AC=AP,M为PB的中点,N在BC上,且BN=| 1 |
| 3 |
(1)求证:MN⊥AB;
(2)求平面MAN与平面PAN的夹角的余弦值.
考点:用空间向量求平面间的夹角
专题:综合题,空间位置关系与距离,空间角
分析:(1)由已知条件推导出△NBA∽△ABC,取AB中点Q,连接MQ、NQ,推导出AB⊥平面MNQ,由此能证明AB⊥MN;
(2)过B作BD∥AC,交AN延长线于D,连PD,分别取PD、AD中点E、F,连ME,EF,MF,可得∠EFM是所求两面角的平面角,即可求平面MAN与平面PAN的夹角的余弦值.
(2)过B作BD∥AC,交AN延长线于D,连PD,分别取PD、AD中点E、F,连ME,EF,MF,可得∠EFM是所求两面角的平面角,即可求平面MAN与平面PAN的夹角的余弦值.
解答:
 (1)证明:设AB=AC=AP=1,又∠BAC=120°,
(1)证明:设AB=AC=AP=1,又∠BAC=120°,
∴在△ABC中,BC2=1+1-2×1×1×cos120°=3,
∴BC=
,
∴BN=
,
∴
=
,
又∠ABC=∠NBA,∴△NBA∽△ABC,
且△NBA也为等腰三角形.
取AB中点Q,连接MQ、NQ,∴NQ⊥AB,MQ∥PAQ,
∵PA⊥面ABC,∴PA⊥AB,∴MQ⊥AB,
∴AB⊥平面MNQ,
又MN?平面MNQ,∴AB⊥MN;
(2)解:过B作BD∥AC,交AN延长线于D,连PD,分别取PD、AD中点E、F,连ME,EF,MF,
由CA⊥面PAD,BD∥AC∥ME,PA⊥AN,EF∥PA,则ME⊥面PAD,EF⊥AN,
且MF⊥AN,∴∠EFM是所求两面角的平面角.
BD=
AC=
,ME=
BD=
,EF=
PA=
,MF=
,
∴cos∠EFM=
.
 (1)证明:设AB=AC=AP=1,又∠BAC=120°,
(1)证明:设AB=AC=AP=1,又∠BAC=120°,∴在△ABC中,BC2=1+1-2×1×1×cos120°=3,
∴BC=
| 3 |
∴BN=
| ||
| 3 |
∴
| AB |
| BC |
| BN |
| AB |
又∠ABC=∠NBA,∴△NBA∽△ABC,
且△NBA也为等腰三角形.
取AB中点Q,连接MQ、NQ,∴NQ⊥AB,MQ∥PAQ,
∵PA⊥面ABC,∴PA⊥AB,∴MQ⊥AB,
∴AB⊥平面MNQ,
又MN?平面MNQ,∴AB⊥MN;
(2)解:过B作BD∥AC,交AN延长线于D,连PD,分别取PD、AD中点E、F,连ME,EF,MF,
由CA⊥面PAD,BD∥AC∥ME,PA⊥AN,EF∥PA,则ME⊥面PAD,EF⊥AN,
且MF⊥AN,∴∠EFM是所求两面角的平面角.
BD=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 2 |
| 1 |
| 2 |
| ||
| 4 |
∴cos∠EFM=
2
| ||
| 5 |
点评:本题考查直线与平面垂直的证明,考查二面角的求法,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
 期末复习检测系列答案
期末复习检测系列答案 超能学典单元期中期末专题冲刺100分系列答案
超能学典单元期中期末专题冲刺100分系列答案 黄冈360度定制密卷系列答案
黄冈360度定制密卷系列答案 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案 名校联盟冲刺卷系列答案
名校联盟冲刺卷系列答案
相关题目
已知圆的方程为x2+y2-6x-8y=0.设该圆过点(-1,4)的最长弦和最短弦分别为AC和BD,则四边形ABCD的面积为( )
| A、15 | B、30 | C、45 | D、60 |
函数f(x)=sinx+cos2x的图象为( )
A、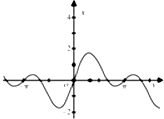 |
B、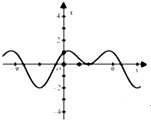 |
C、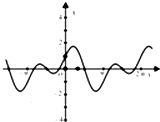 |
D、 |
