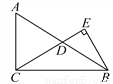
如图，在Rt△ABC中，∠ACB＝90°，D是边AB的中点，BE⊥CD，垂足为点E.已知AC＝15，cosA＝
.
(1)求线段CD的长；
(2)求sin∠DBE的值．
（1）CD＝；（2）sin∠DBE=.
【解析】试题分析：（1）根据直角三角形斜边上的中线等于斜边的一半，求出AB的长，即可求出CD的长；（2）由于D为AB上的中点，求出AD=BD=CD=，设DE=x，EB=y，利用勾股定理即可求出x的值，据此解答即可．
试题解析：：【解析】
（1）∵AC=15，cosA=，
∴cosA=,
∴AB=25，
∵△ACB为直角三角形，... 下列各组条件中，能判断两个直角三角形全等的是( )
A. 一组边对应相等 B. 两组直角边对应相等
C. 两组锐角对应相等 D. 一组锐角对应相等
B
【解析】A、两直角三角形隐含一个条件是两直角相等，现已知一组边对应相等 ，要判定两直角三角形全等，还需要一组角对应相等地或是另一组边对应相等才能进行判定，故选项错误；
B、可以利用边角边判定两三角形全等，故本选项正确；
C、两个锐角分别相等，只有角没有边，不能判定全等，此选项错误；
D、一组锐角对应相等，隐含一个条件是两直角相等，根据角对应相等，不能判定三角形全等，故选... 如图，∠C＝∠D＝90°，若添加一个条件，可使用“HL”判定Rt△ABC与Rt△ABD全等，则以下给出的条件适合的是( )
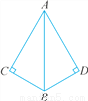
A. AC＝AD B. AB＝AB C. ∠ABC＝∠ABD D. ∠BAC＝∠BAD
A
【解析】根据题意可知∠C=∠D=90°，AB=AB，
然后由AC=AD，可根据HL判定两直角三角形全等，故符合条件；
而B答案只知道一边一角，不能够判定两三角形全等，故不正确；
C答案符合AAS，证明两三角形全等，故不正确；
D答案是符合AAS，能证明两三角形全等，故不正确.
故选：A. 如图所示，在Rt△ACD和Rt△BCE中，若AD＝BE，DC＝EC，则无法得出的结论是( )
A. OA＝OB B. E是AC的中点 C. △AOE≌△BOD D. AE＝BD
B
【解析】∵∠C=∠C=90°，
∴△ACD和△BCE是直角三角形，
在Rt△ACD和Rt△BCE中，
∴Rt△ACD≌Rt△BCE（HL），
∴∠B=∠A，CB=CA，
∵CD=CE，
∴AE=BD，故D正确，
在△AOE和△BOD中，
∴△AOE≌△BOD（AAS），故C正确，
∴AO=OB，故A正确，
AE=BD，CE=CD... 如图，在△ABC中，AD⊥BC于D，BE⊥AC于E，AD与BE相交于点F，若BF=AC，则∠ABC＝______度．
45
【解析】试题分析：根据三角形全等的判定和性质，先证△ADC≌△BDF，可得BD=AD，再根据等腰直角三角形的性质可求∠ABC=∠BAD=45°．
【解析】
∵AD⊥BC于D，BE⊥AC于E
∴∠EAF+∠AFE=90°,∠DBF+∠BFD=90°，
又∵∠BFD=∠AFE(对顶角相等)
∴∠EAF=∠DBF，
在Rt△ADC和Rt△BDF中，
，
... 如图，过正方形ABCD的顶点B作直线l，过点A，C作l的垂线，垂足分别为点E，F．若AE＝2，CF＝6，则AB的长度为 ．
．
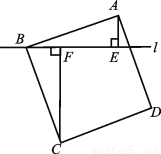
【解析】
试题分析：∵四边形ABCD是正方形，
∴∠CBF+∠FBA=90°，∠CBF+∠BCF=90°，
∴∠BCF=∠ABE，
∵∠AEB=∠BFC=90°，AB=BC，
∴△ABE≌△BCF（AAS）
∴AE=BF，BE=CF，
∴AB=．
故答案是． 如图，有一个直角△ABC，∠C=90°，AC=10，BC=5，一条线段PQ=AB，P.Q两点分别在AC和过点A且垂直于AC的射线AX上运动，当AP= 时,才能使ΔABC≌ΔPQA.
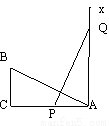
10
【解析】
试题分析：要使△ABC≌△PQA，根据全等三角形的性质可得AP=CA，则说明当P运动到C时，利用直角三角形全等的判定HL可证△ABC≌△PQA．
∵AX⊥AC，∠C=90°，
∴∠C=∠PAQ=90°，
又∵AP=CB=5，PQ=AB，
∴△ABC≌△PQA．
点P运动到C点时，△ABC≌△PQA．
∵AX⊥AC，∠C=90°，
... 如图，在Rt△ABC和Rt△A′B′C′中，∠C＝∠C′＝90°，那么在下列各条件中，不能判定Rt△ABC≌Rt△A′B′C′的是( )
A. AB＝A′B′＝5，BC＝B′C′＝3 B. AB＝B′C′＝5，∠A＝∠B′＝40°
C. AC＝A′C′＝5，BC＝B′C′＝3 D. AC＝A′C′＝5，∠A＝∠A′＝40°
B
【解析】∵在Rt△ABC和Rt△A′B′C′中，∠C=∠C′=90°
A选项：AB=A′B′=5，BC=B′C′=3，
符合直角三角形全等的判定条件HL，
∴A选项能使Rt△ABC≌Rt△A′B′C′；
B选项：AB=B′C′=5，∠A=∠B′=40°，
不符合符合直角三角形全等的判定条件，
∴B选项不能使Rt△ABC≌Rt△A′B′C′；
C选项符合Rt△ABC和Rt△A... 在两个直角三角形中，若有一对角(非直角)相等，一对边相等，则两个直角三角形( )
A. 一定全等 B. 一定不全等 C. 不一定全等 D. 以上都不是
C
【解析】如果有一对角(非直角)对应相等，一对边对应相等，题中还隐含着一对直角相等，则这两个三角形一定全等，
若不是对应相等，则不一定全等，
故选C. 如图所示，在四边形ABCD中，CB=CD，∠ABC=∠ADC=90°，∠BAC=35°，则∠BCD的度数为 ________度．
110
【解析】∵∠ABC=∠ADC=90°，CB=CD，且CA=CA，
∴△ABC≌△ADC，
∴∠BCA=∠DCA，
∵∠BAC=35°，∠ABC=90°，
∴∠BCA=55°，
∴∠BCD=2∠BCA=110°，
故答案为：110．