题目内容
如图所示,在Rt△ACD和Rt△BCE中,若AD=BE,DC=EC,则无法得出的结论是( )

A. OA=OB B. E是AC的中点 C. △AOE≌△BOD D. AE=BD
 B
【解析】∵∠C=∠C=90°,
∴△ACD和△BCE是直角三角形,
在Rt△ACD和Rt△BCE中,
∴Rt△ACD≌Rt△BCE(HL),
∴∠B=∠A,CB=CA,
∵CD=CE,
∴AE=BD,故D正确,
在△AOE和△BOD中,
∴△AOE≌△BOD(AAS),故C正确,
∴AO=OB,故A正确,
AE=BD,CE=CD...
B
【解析】∵∠C=∠C=90°,
∴△ACD和△BCE是直角三角形,
在Rt△ACD和Rt△BCE中,
∴Rt△ACD≌Rt△BCE(HL),
∴∠B=∠A,CB=CA,
∵CD=CE,
∴AE=BD,故D正确,
在△AOE和△BOD中,
∴△AOE≌△BOD(AAS),故C正确,
∴AO=OB,故A正确,
AE=BD,CE=CD...
下面是网球场地,A、B、C、D、E、F几个区域中,其中全等图形的对数为()
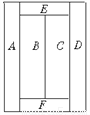
A. 1 B. 2 C. 3 D. 4
 C
【解析】图中六个长方形正好三对,图中A与D、B与C、E与F正好两两全等,
故选C.
C
【解析】图中六个长方形正好三对,图中A与D、B与C、E与F正好两两全等,
故选C. 如图,线段AD把△ABC分为面积相等的两部分,则线段AD是( ).
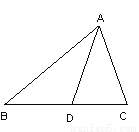
A. 三角形的角平分线 B. 三角形的中线
C. 三角形的高 D. 以上都不对
 B
【解析】试题分析:三角形的中线将三角形的面积分成相等的两部分,角平分线是指将角分成度数相等的两个角.
B
【解析】试题分析:三角形的中线将三角形的面积分成相等的两部分,角平分线是指将角分成度数相等的两个角. 下列说法中:
①P是线段AB上的一点,直线l经过点P且l⊥AB,则l是线段AB的垂直平分线;
②直线l经过线段AB的中点,则l是线段AB的垂直平分线;
③若AP=PB,且直线l垂直于线段AB,则l是线段AB的垂直平分线;
④经过线段AB的中点P且垂直于AB的直线l是线段AB的垂直平分线.
其中正确的有( )
A. 1个 B. 2个 C. 3个 D. 4个
 A
【解析】根据线段的垂直平分线的定义,以及定理:到线段的两端距离相等的点在线段的垂直平分线上,即可判断.
【解析】
①当P不是AB的中点,则直线l不平分线段AB,故错误;
②直线l经过线段AB的中点,且垂直于AB则l是线段AB的垂直平分线,故错误;
③若AP=PB,则P在线段AB的垂直平分线上,但l不一定过点P,所以直线l不一定是线段AB的垂直平分线,故错误;
④...
A
【解析】根据线段的垂直平分线的定义,以及定理:到线段的两端距离相等的点在线段的垂直平分线上,即可判断.
【解析】
①当P不是AB的中点,则直线l不平分线段AB,故错误;
②直线l经过线段AB的中点,且垂直于AB则l是线段AB的垂直平分线,故错误;
③若AP=PB,则P在线段AB的垂直平分线上,但l不一定过点P,所以直线l不一定是线段AB的垂直平分线,故错误;
④... 在两个直角三角形中,若有一对角(非直角)相等,一对边相等,则两个直角三角形( )
A. 一定全等 B. 一定不全等 C. 不一定全等 D. 以上都不是
 C
【解析】如果有一对角(非直角)对应相等,一对边对应相等,题中还隐含着一对直角相等,则这两个三角形一定全等,
若不是对应相等,则不一定全等,
故选C.
C
【解析】如果有一对角(非直角)对应相等,一对边对应相等,题中还隐含着一对直角相等,则这两个三角形一定全等,
若不是对应相等,则不一定全等,
故选C. 在△ABC中,∠C=90°,cosA=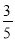 ,AC=6.求△ABC的周长和面积.
,AC=6.求△ABC的周长和面积.
 周长为24,面积为24.
【解析】试题分析:根据余弦的定义求出斜边AB的长,再根据勾股定理求出BC的长,再根据三角形的周长、面积的求法即可得.
试题解析:∵∠C=90°,∴cosA=,
∵cosA=,AC=6,
∴AB=10,
∴BC==8,
∴△ABC的周长=AC+BC+AB=6+8+10=24,
S△ABC==24.
周长为24,面积为24.
【解析】试题分析:根据余弦的定义求出斜边AB的长,再根据勾股定理求出BC的长,再根据三角形的周长、面积的求法即可得.
试题解析:∵∠C=90°,∴cosA=,
∵cosA=,AC=6,
∴AB=10,
∴BC==8,
∴△ABC的周长=AC+BC+AB=6+8+10=24,
S△ABC==24. 如图,菱形ABCD的周长为20cm,DE⊥AB,垂足为E,cosA=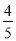 ,则下列结论中正确的个数为( )
,则下列结论中正确的个数为( )
①DE=3cm;②EB=1cm;③S菱形ABCD=15cm2
.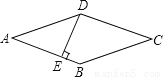
A.3个 B.2个 C.1个 D.0个
 A.
【解析】
试题解析:由题意可得,菱形的边长为5cm,又cosA=,所以AE=4,
则DE=3cm;EB=1cm;S菱形ABCD=5×3=15cm2,
故选A.
A.
【解析】
试题解析:由题意可得,菱形的边长为5cm,又cosA=,所以AE=4,
则DE=3cm;EB=1cm;S菱形ABCD=5×3=15cm2,
故选A. 在△ABC中,若|sinA-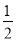 |+(
|+(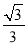 -tanB)2=0,则∠C的度数为( )
-tanB)2=0,则∠C的度数为( )
A. 30° B. 60° C. 90° D. 120°
 D
【解析】试题解析:∵|sinA-|+(-tanB)2=0,
∴|sinA-|=0,( -tanB)2=0,
∴sinA-=0, -tanB=0,
sinA=,tanB=
∴∠A=30°,∠B=30°,
∴∠C=120°.
故选D.
D
【解析】试题解析:∵|sinA-|+(-tanB)2=0,
∴|sinA-|=0,( -tanB)2=0,
∴sinA-=0, -tanB=0,
sinA=,tanB=
∴∠A=30°,∠B=30°,
∴∠C=120°.
故选D. 下列语句中,正确的个数有( )
①两个关于某直线对称的图形是全等的
②两个图形关于某直线对称,对称点一定在该直线的两旁
③两个成轴对称的图形的对应点连线的垂直平分线,就是它们的对称轴
④平面内两个全等的图形一定关于某直线对称.
A. 1个 B. 2个 C. 3个 D. 4个
 B
【解析】【解析】
①两个关于某直线对称的图形是全等的,此选项正确;
②两个图形关于某直线对称,对称点一定在该直线的两旁也有可能在直线上,此选项错误;
③两个成轴对称的图形的对应点连线的垂直平分线,就是它们的对称轴,此选项正确;
④平面内两个全等的图形不一定关于某直线对称,故此选项错误.
故选B.
B
【解析】【解析】
①两个关于某直线对称的图形是全等的,此选项正确;
②两个图形关于某直线对称,对称点一定在该直线的两旁也有可能在直线上,此选项错误;
③两个成轴对称的图形的对应点连线的垂直平分线,就是它们的对称轴,此选项正确;
④平面内两个全等的图形不一定关于某直线对称,故此选项错误.
故选B. 
