��Ŀ����
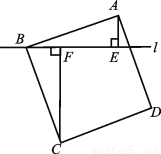
��ͼ����������ABCD�Ķ���B��ֱ��l������A��C��l�Ĵ��ߣ�����ֱ�Ϊ��E��F����AE��2��CF��6����AB�ij���Ϊ ��
 ��
��������
������������ı���ABCD�������Σ�
���CBF+��FBA=90�㣬��CBF+��BCF=90�㣬
���BCF=��ABE��
�ߡ�AEB=��BFC=90�㣬AB=BC��
���ABE�ա�BCF��AAS��
��AE=BF��BE=CF��
��AB=��
�ʴ��ǣ�
��
��������
������������ı���ABCD�������Σ�
���CBF+��FBA=90�㣬��CBF+��BCF=90�㣬
���BCF=��ABE��
�ߡ�AEB=��BFC=90�㣬AB=BC��
���ABE�ա�BCF��AAS��
��AE=BF��BE=CF��
��AB=��
�ʴ��ǣ�
 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д���ͼ��ijͬѧ��һ�������εIJ�������������飬����Ҫ��������ȥ��һ����ȫһ���IJ�������ô��ʡ�µİ취�ǣ� ��
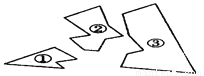
A. ����ȥ B. ����ȥ C. ����ȥ D. ���ٺ͢�ȥ
 C
�����������������A������ȥ����������ԭ�����ε�һ���ǺͲ��ֱߣ����ܵõ���ԭ��һ���������Σ���Aѡ�����
B������ȥ����������ԭ�����ε�һ���ֱߣ�Ҳ�Dz��ܵõ���ԭ��һ���������Σ���Bѡ�����
C������ȥ������������ԭ�����ε������ǻ�����������һ���ߣ�����ASA�ж�����Cѡ����ȷ��
D�����ٺ͢�ȥ����������ԭ�����ε�һ���ǺͲ��ֱߣ�ͬ�����ܵõ���ԭ��һ���������Σ���D...
C
�����������������A������ȥ����������ԭ�����ε�һ���ǺͲ��ֱߣ����ܵõ���ԭ��һ���������Σ���Aѡ�����
B������ȥ����������ԭ�����ε�һ���ֱߣ�Ҳ�Dz��ܵõ���ԭ��һ���������Σ���Bѡ�����
C������ȥ������������ԭ�����ε������ǻ�����������һ���ߣ�����ASA�ж�����Cѡ����ȷ��
D�����ٺ͢�ȥ����������ԭ�����ε�һ���ǺͲ��ֱߣ�ͬ�����ܵõ���ԭ��һ���������Σ���D... ���������У����ж���ABCΪֱ�������ε���( )
A. ��A=��B=��C B. ��A����B=2��C
C. ��A�á�B�á�C=1��2��3 D. ��A=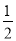 ��B=
��B=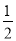 ��C
��C
 C
�����������������A. ����A=��B=��C����ȷ����ABCΪֱ�������Σ�����Aѡ�����
B�� ,����A+��B=2��C,������Bѡ�����
C. ,����A�á�B�á�C=1��2��3,������Cѡ����ȷ��
D. ����������Dѡ�����.
��ѡC.
C
�����������������A. ����A=��B=��C����ȷ����ABCΪֱ�������Σ�����Aѡ�����
B�� ,����A+��B=2��C,������Bѡ�����
C. ,����A�á�B�á�C=1��2��3,������Cѡ����ȷ��
D. ����������Dѡ�����.
��ѡC. ��֪��ABC���ܳ���l,BC=l-2AB,������ֱ��һ��Ϊ��ABC�ĶԳ������(����)
A. ��ABC�ı�AB�Ĵ�ֱƽ���� B. ��ACB��ƽ�������ڵ�ֱ��
C. ��ABC�ı�BC�ϵ��������ڵ�ֱ�� D. ��ABC�ı�AC�ϵĸ����ڵ�ֱ��
 C
���������������������Ƴ�AB=AC���ɴ˼����жϣ�
��������
��l=AB+BC+AC��
��BC=l?2AB=AB+BC+AC?2AB��
��AB=AC��
���ABC��BC���������ڵ�ֱ���ǡ�ABC�ĶԳ���.
��ѡC.
C
���������������������Ƴ�AB=AC���ɴ˼����жϣ�
��������
��l=AB+BC+AC��
��BC=l?2AB=AB+BC+AC?2AB��
��AB=AC��
���ABC��BC���������ڵ�ֱ���ǡ�ABC�ĶԳ���.
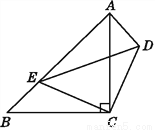
��ѡC. ��ͼ,��ABC,��CDE��Ϊ����ֱ��������,��ACB=��DCE=90��,��E��AB��,��˵��:��CDA�ա�CEB.
 �𰸼�����
��������������������ݵ���ֱ�������ε����ʵó�CE=CD��BC=AC��������ȫ�������ε��ж�֤�����ɣ�
���������֤�����ߡ�ABC����CDE��Ϊ����ֱ�������Σ���ACB=��DCE=90�㣬
��CE=CD��BC=AC��
���ACB����ACE=��DCE����ACE��
���ECB=��DCA��
�ڡ�CDA���CEB�У� ��
���CDA�ա�CEB��
�𰸼�����
��������������������ݵ���ֱ�������ε����ʵó�CE=CD��BC=AC��������ȫ�������ε��ж�֤�����ɣ�
���������֤�����ߡ�ABC����CDE��Ϊ����ֱ�������Σ���ACB=��DCE=90�㣬
��CE=CD��BC=AC��
���ACB����ACE=��DCE����ACE��
���ECB=��DCA��
�ڡ�CDA���CEB�У� ��
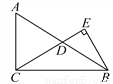
���CDA�ա�CEB�� ��ͼ����Rt��ABC�У���ACB��90�㣬D�DZ�AB���е㣬BE��CD������Ϊ��E.��֪AC��15��cosA�� .
.
(1)���߶�CD�ij���
(2)��sin��DBE��ֵ��
 ��1��CD������2��sin��DBE=.
�������������������1������ֱ��������б���ϵ����ߵ���б�ߵ�һ�룬���AB�ij����������CD�ij�����2������DΪAB�ϵ��е㣬���AD=BD=CD=����DE=x��EB=y�����ù��ɶ����������x��ֵ���ݴ˽�ɣ�
�������������������
��1����AC=15��cosA=��
��cosA=,
��AB=25��
�ߡ�ACBΪֱ�������Σ�...
��1��CD������2��sin��DBE=.
�������������������1������ֱ��������б���ϵ����ߵ���б�ߵ�һ�룬���AB�ij����������CD�ij�����2������DΪAB�ϵ��е㣬���AD=BD=CD=����DE=x��EB=y�����ù��ɶ����������x��ֵ���ݴ˽�ɣ�
�������������������
��1����AC=15��cosA=��
��cosA=,
��AB=25��
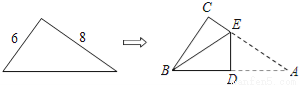
�ߡ�ACBΪֱ�������Σ�... ֱ��������ֽƬ����ֱ�DZ߳��ֱ�Ϊ6��8���ֽ���ABC��ͼ�����۵���ʹ��A���B�غϣ��ۺ�ΪDE����tan��CBE��ֵ�ǣ� ��
A. 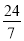 B.
B. 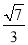 C.
C. 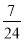 D.
D. 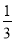
 C
����������������������۵��任�����ʿ�֪AE=BE����CE=x����֪BE=8-x�����ݹ��ɶ����ã��������x=����˿���tan��CBE=��
��ѡC
C
����������������������۵��任�����ʿ�֪AE=BE����CE=x����֪BE=8-x�����ݹ��ɶ����ã��������x=����˿���tan��CBE=��
��ѡC ��Rt��ABC�У���C��90�㣬����˵����ȷ����( )
��sinA��cosA����sin2A��cos2A��1����tanA��tanB��1����tanA��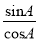
A. �٢ڢ� B. �ڢۢ� C. �٢ۢ� D. �٢ڢۢ�
 B
���������ߡ�C=90�㣬�࣬��֪�в�֪BC��AC�ڴ�С��ϵ���ʢٴ���
���ʢ���ȷ��
���ʢ���ȷ��
���ʢ���ȷ��
��ѡB.
B
���������ߡ�C=90�㣬�࣬��֪�в�֪BC��AC�ڴ�С��ϵ���ʢٴ���
���ʢ���ȷ��
���ʢ���ȷ��
���ʢ���ȷ��
��ѡB. ��֪��ABC����ֱ��MN�Գƣ�������˵��������ǣ�������
A. ��ABC�б���һ��������ֱ��MN��
B. ��ABC������������
C. ��ABC���������������
D. ��ABC�б�����һ���ǵ���60��
 D
����������������
�ߡ�ABC����ֱ��MN�Գƣ����ABCΪ���������Σ���Գ���Ϊ�ױ��ϵĸ����ڵ�ֱ�ߣ�
A����ABC�б���һ��������ֱ��MN�ϣ��ʱ�ѡ����ȷ��
B����ABC�б�����������ȣ��ʱ�ѡ����ȷ��
C����ABC�У�������������ȣ��ʱ�ѡ����ȷ��
D�����õ����������ǵȱ�������ʱ����ABC����һ���ǵ���60�㣬�ʱ�ѡ�����
��ѡD��
D
����������������
�ߡ�ABC����ֱ��MN�Գƣ����ABCΪ���������Σ���Գ���Ϊ�ױ��ϵĸ����ڵ�ֱ�ߣ�
A����ABC�б���һ��������ֱ��MN�ϣ��ʱ�ѡ����ȷ��
B����ABC�б�����������ȣ��ʱ�ѡ����ȷ��
C����ABC�У�������������ȣ��ʱ�ѡ����ȷ��
D�����õ����������ǵȱ�������ʱ����ABC����һ���ǵ���60�㣬�ʱ�ѡ�����
��ѡD�� 
