题目内容
如图,∠C=∠D=90°,若添加一个条件,可使用“HL”判定Rt△ABC与Rt△ABD全等,则以下给出的条件适合的是( )
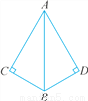
A. AC=AD B. AB=AB C. ∠ABC=∠ABD D. ∠BAC=∠BAD
 A
【解析】根据题意可知∠C=∠D=90°,AB=AB,
然后由AC=AD,可根据HL判定两直角三角形全等,故符合条件;
而B答案只知道一边一角,不能够判定两三角形全等,故不正确;
C答案符合AAS,证明两三角形全等,故不正确;
D答案是符合AAS,能证明两三角形全等,故不正确.
故选:A.
A
【解析】根据题意可知∠C=∠D=90°,AB=AB,
然后由AC=AD,可根据HL判定两直角三角形全等,故符合条件;
而B答案只知道一边一角,不能够判定两三角形全等,故不正确;
C答案符合AAS,证明两三角形全等,故不正确;
D答案是符合AAS,能证明两三角形全等,故不正确.
故选:A.
下列图形能分成两个全等图形的是()
A. 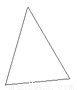
B. 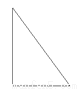
C. 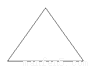
D. 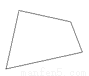
 C
【解析】全等图形需要大小相等,形状相同,原图中只有C是一个等腰三角形可以分成两个全等的直角三角形,A、B、D都不符合要求,
故选C.
C
【解析】全等图形需要大小相等,形状相同,原图中只有C是一个等腰三角形可以分成两个全等的直角三角形,A、B、D都不符合要求,
故选C. 如果一个三角形三条高的交点在三角形外部,那么这个三角形是( )
A. 锐角三角形 B. 钝角三角形
C. 直角三角形 D. 无法确定
 B
【解析】试题解析:由题意可知,如果一个三角形的三条高的交点在三角形外部,那么这个三角形是钝角三角形;
故选B.
B
【解析】试题解析:由题意可知,如果一个三角形的三条高的交点在三角形外部,那么这个三角形是钝角三角形;
故选B. 如图,∠ABC=∠ADE=90°,AD=AB,AC=AE,BC与DE相交于点F,连接CD、EB.
(1)图中共有几对全等三角形,请你一一列举;
(2)求证:CF=EF.
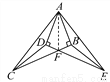
 (1)有三对全等三角形,具体见解析;(2)证明见解析.
【解析】试题分析:(1)根据全等三角形的判定,结合图形得出即可;
(2)连接AF,根据HL证Rt△ABC≌Rt△ADE推出BC=DE,根据HL推出△ADF≌△ABF,推出DF=BF,利用线段的差即可得.
试题解析:(1) 图中有3对全等三角形有Rt△ABC≌Rt△ADE,△ACD≌△AEB,△CDF≌△EBF;
(2)...
(1)有三对全等三角形,具体见解析;(2)证明见解析.
【解析】试题分析:(1)根据全等三角形的判定,结合图形得出即可;
(2)连接AF,根据HL证Rt△ABC≌Rt△ADE推出BC=DE,根据HL推出△ADF≌△ABF,推出DF=BF,利用线段的差即可得.
试题解析:(1) 图中有3对全等三角形有Rt△ABC≌Rt△ADE,△ACD≌△AEB,△CDF≌△EBF;
(2)... 如图,在Rt△ABC和Rt△A′B′C′中,∠C=∠C′=90°,那么在下列各条件中,不能判定Rt△ABC≌Rt△A′B′C′的是( )

A. AB=A′B′=5,BC=B′C′=3 B. AB=B′C′=5,∠A=∠B′=40°
C. AC=A′C′=5,BC=B′C′=3 D. AC=A′C′=5,∠A=∠A′=40°
 B
【解析】∵在Rt△ABC和Rt△A′B′C′中,∠C=∠C′=90°
A选项:AB=A′B′=5,BC=B′C′=3,
符合直角三角形全等的判定条件HL,
∴A选项能使Rt△ABC≌Rt△A′B′C′;
B选项:AB=B′C′=5,∠A=∠B′=40°,
不符合符合直角三角形全等的判定条件,
∴B选项不能使Rt△ABC≌Rt△A′B′C′;
C选项符合Rt△ABC和Rt△A...
B
【解析】∵在Rt△ABC和Rt△A′B′C′中,∠C=∠C′=90°
A选项:AB=A′B′=5,BC=B′C′=3,
符合直角三角形全等的判定条件HL,
∴A选项能使Rt△ABC≌Rt△A′B′C′;
B选项:AB=B′C′=5,∠A=∠B′=40°,
不符合符合直角三角形全等的判定条件,
∴B选项不能使Rt△ABC≌Rt△A′B′C′;
C选项符合Rt△ABC和Rt△A... 如图,在Rt△ABC中,BC、AC、AB三边的长分别为a、b、c,则sinA=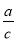 ,cosA=
,cosA=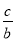 ,tanA=
,tanA=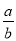 .我们不难发现:sin260°+cos260°=1,…,试探求sinA、cosA、tanA之间存在的一般关系,并说明理由.
.我们不难发现:sin260°+cos260°=1,…,试探求sinA、cosA、tanA之间存在的一般关系,并说明理由.
 sin2A+cos2A=1,tanA=,理由见解析.
【解析】试题分析:sin2A+cos2A=1,tanA=,根据三角函数的定义以及勾股定理通过推导即可得.
试题解析:sin2A+cos2A=1,tanA=,理由如下:
∵∠C=90°,∴a2+b2=c2,sinA=,cosA=,tanA=,
∴sin2A+cos2A=;
tanA=..
sin2A+cos2A=1,tanA=,理由见解析.
【解析】试题分析:sin2A+cos2A=1,tanA=,根据三角函数的定义以及勾股定理通过推导即可得.
试题解析:sin2A+cos2A=1,tanA=,理由如下:
∵∠C=90°,∴a2+b2=c2,sinA=,cosA=,tanA=,
∴sin2A+cos2A=;
tanA=.. 如图,在Rt△ABC中,∠ACB=90°,CD⊥AB,垂足为D.若AC=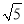 ,BC=2,则sin∠ACD的值为( )
,BC=2,则sin∠ACD的值为( )
A. 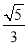 B.
B. 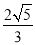 C.
C. 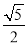 D.
D. 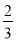
 A
【解析】在Rt△ABC中,根据勾股定理可得:
AB===3.
∵∠B+∠BCD=90°,∠ACD+∠BCD=90°,
∴∠B=∠ACD,
∴sin∠ACD=sin∠B==.
故选A.
A
【解析】在Rt△ABC中,根据勾股定理可得:
AB===3.
∵∠B+∠BCD=90°,∠ACD+∠BCD=90°,
∴∠B=∠ACD,
∴sin∠ACD=sin∠B==.
故选A. 计算6tan45°-2cos60°的结果是()
A. 4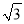 B. 4 C. 5
B. 4 C. 5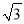 D. 5
D. 5
 D
【解析】试题分析:将特殊角的三角函数值代入计算即可:原式.故选D.
D
【解析】试题分析:将特殊角的三角函数值代入计算即可:原式.故选D. 如图,正六边形ABCDEF关于直线l的轴对称图形是六边形A′B′C′D′E′F′,下列判断错误的是( ).
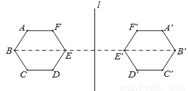
A.AB=A′B′ B.BC∥B′C′ C.直线l⊥BB′ D.∠A′=120°
 B.
【解析】
试题分析:关于轴对称的两个图形沿对称轴翻折,能够重合,两个图形是全等形,对应边相等,所以A正确;C正确,因为正六边形的一个内角是120度,所以D正确.故本题选B.
B.
【解析】
试题分析:关于轴对称的两个图形沿对称轴翻折,能够重合,两个图形是全等形,对应边相等,所以A正确;C正确,因为正六边形的一个内角是120度,所以D正确.故本题选B. 
