题目内容
如图，在Rt△ABC和Rt△A′B′C′中，∠C＝∠C′＝90°，那么在下列各条件中，不能判定Rt△ABC≌Rt△A′B′C′的是( )
A. AB＝A′B′＝5，BC＝B′C′＝3 B. AB＝B′C′＝5，∠A＝∠B′＝40°
C. AC＝A′C′＝5，BC＝B′C′＝3 D. AC＝A′C′＝5，∠A＝∠A′＝40°
B
【解析】∵在Rt△ABC和Rt△A′B′C′中，∠C=∠C′=90°
A选项：AB=A′B′=5，BC=B′C′=3，
符合直角三角形全等的判定条件HL，
∴A选项能使Rt△ABC≌Rt△A′B′C′；
B选项：AB=B′C′=5，∠A=∠B′=40°，
不符合符合直角三角形全等的判定条件，
∴B选项不能使Rt△ABC≌Rt△A′B′C′；
C选项符合Rt△ABC和Rt△A...
下列图中，与左图中的图案完全一致的是（）
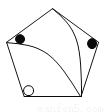
A.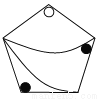 
B.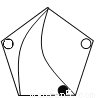 
C.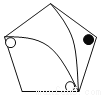 
D.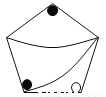 
A
【解析】A图案可以通过旋转得到，故A符合题意；B、C、D通过旋转、平移都不能得到，
故选A. 如图，为测量B点到河对面的目标A之间的距离，他们在B点同侧选择了一点C，测得∠ABC＝70°，∠ACB＝40°，然后在M处立了标杆，使∠CBM＝70°，∠BCM＝40°，那么需要测量________才能测得A，B之间的距离( )
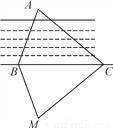
A. AB B. AC C. BM D. CM
C
【解析】∵∠ABC=∠CBM=70°，BC=BC，∠ACB=∠MCB=40°，
∴△ABC≌△MBC，∴AB=BM，
所以需要测量BM的长才能测得A、B之间的距离，
故选C. 如图，四边形ABCD中，AC垂直平分BD，垂足为E，下列结论不一定成立的是（ ）
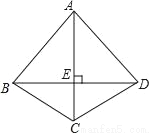
A. AB=AD B. AC平分∠BCD C. AB=BD D. △BEC≌△DEC
C
【解析】试题分析：根据AC垂直平分BD可得：△ABD为等腰三角形，即AB=AD，AC平分∠BAD，△BEC≌△DEC. 杨阳同学沿一段笔直的人行道行走,在由A步行到达B处的过程中,通过隔离带的空隙O,刚好浏览完对面人行道宣传墙上的社会主义核心价值观标语,其具体信息汇集如下:
如图,AB∥OH∥CD,相邻两平行线间的距离相等,AC,BD相交于O,OD⊥CD,垂足为D,已知AB=20米,请根据上述信息求标语CD的长度.
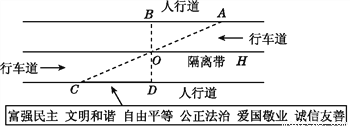
20米.
【解析】试题分析：已知AB∥CD，根据平行线的性质可得∠ABO=∠CDO，再由垂直的定义可得∠CDO=90°，可得OB⊥AB，根据相邻两平行线间的距离相等可得OD=OB，即可根据ASA定理判定△ABO≌△CDO，由全等三角形的性质即可得CD=AB=20m．
试题解析：∵AB∥CD，∴∠ABO=∠CDO，
∵OD⊥CD，∴∠CDO=90°，
∴∠ABO=90°，即O... 如图，∠C＝∠D＝90°，若添加一个条件，可使用“HL”判定Rt△ABC与Rt△ABD全等，则以下给出的条件适合的是( )
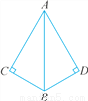
A. AC＝AD B. AB＝AB C. ∠ABC＝∠ABD D. ∠BAC＝∠BAD
A
【解析】根据题意可知∠C=∠D=90°，AB=AB，
然后由AC=AD，可根据HL判定两直角三角形全等，故符合条件；
而B答案只知道一边一角，不能够判定两三角形全等，故不正确；
C答案符合AAS，证明两三角形全等，故不正确；
D答案是符合AAS，能证明两三角形全等，故不正确.
故选：A. 如图，在四边形ABCD中，E、F分别是AB、AD的中点．若EF＝2，BC＝5，CD＝3，则cosC的值为_______．
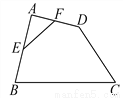
【解析】连接BD，
∵E、F分别是AB、AD的中点，
∴EF∥BD，且BD=2EF=4，
∵BD=4，BC=5，CD=3，
∴△BDC是直角三角形，
∴tan C=，
故答案为： . 在Rt△ABC中，∠C＝90°，AB＝2BC，现给出下列结论：①sinA＝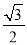
；②cosB＝
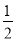；③tanA＝
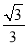；④tanB＝
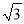，其中正确的结论是_____ .
②③④
【解析】∵在Rt△ABC中，∠C=90°，AB=2BC，∴。∴∠A=30°。∴∠B=60°。
∴cosB= cos60°=，tanA= tan300=，tanB= tan600=。
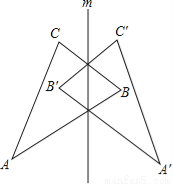
∴正确的结论是②③④。 如图，△ABC和△A′B′C′关于直线m对称．
（1）结合图形指出对称点．
（2）连接A、A′，直线m与线段AA′有什么关系？
（3）延长线段AC与A′C′，它们的交点与直线m有怎样的关系？其它对应线段（或其延长线）的交点呢？你发现了什么规律，请叙述出来与同伴交流．
【解析】
（1）对称点有A和A'，B和B'，C和C'．
（2）连接A、A′，直线m是线段AA′的垂直平分线．
（3）延长线段AC与A′C′，它们的交点在直线m上，其它对应线段（或其延长线）的交点也在直线m上，
即若两线段关于直线m对称，且不平行，则它们的交点或它们的延长线的交点在对称轴上．
【解析】本题考查轴对称图形的定义，如果一个图形沿着一条直线对折，两侧的图形能完全重...