题目内容
在两个直角三角形中，若有一对角(非直角)相等，一对边相等，则两个直角三角形( )
A. 一定全等 B. 一定不全等 C. 不一定全等 D. 以上都不是
C
【解析】如果有一对角(非直角)对应相等，一对边对应相等，题中还隐含着一对直角相等，则这两个三角形一定全等，
若不是对应相等，则不一定全等，
故选C.
练习册系列答案
智慧小复习系列答案
相关题目
如图，△AOD关于直线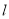
进行轴对称变换后得到△BOC，下列不正确的是（）.
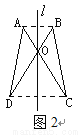
A. ∠DAO=∠CBO，∠ADO=∠BCO B. 直线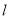
垂直平分AB、CD
C. △AO D和△BOC均是等腰三角形 D. AD=BC，OD=OC
C
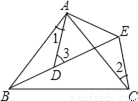
【解析】试题分析：根据轴对称图形的性质可得：A、B、D为正确答案；△OAB和△DOC为等腰三角形. 如图所示， AB=AC，AD=AE，∠BAC=∠DAE，∠1=25°，∠2=30°，则∠3=_____.
55°
【解析】求出∠BAD=∠EAC，证△BAD≌△EAC，推出∠2=∠ABD=30°，根据三角形的外角性质求出即可．
【解析】
∵∠BAC=∠DAE，
∴∠BAC﹣∠DAC=∠DAE﹣∠DAC，
∴∠1=∠EAC，
在△BAD和△EAC中，
AB=AC，∠BAD=∠EAC，
∴△BAD≌△EAC（SAS），
∴∠2=∠ABD=30°，
∵... △ABC中，AB = 5，AC = 6，BC = 4，边AB的垂直平分线交AC于点D，则△BDC的周长是（ ）
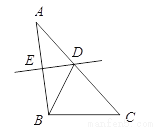
A. 8 B. 9 C. 10 D. 11
C
【解析】试题分析：由ED是AB的垂直平分线，可得AD=BD，又由△BDC的周长=DB+BC+CD，即可得△BDC的周长=AD+BC+CD=AC+BC． ∵ED是AB的垂直平分线， ∴AD=BD，
∵△BDC的周长=DB+BC+CD， ∴△BDC的周长=AD+BC+CD=AC+BC=6+4=10． （2011•江津区）在△ABC中，AB=CB，∠ABC=90°，F为AB延长线上一点，点E在BC上，且AE=CF．
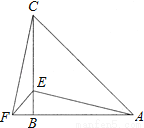
（1）求证：Rt△ABE≌Rt△CBF；
（2）若∠CAE=30°，求∠ACF的度数．
（1）见解析；（2）60°．
【解析】
试题分析：（1）由AB=CB，∠ABC=90°，AE=CF，即可利用HL证得Rt△ABE≌Rt△CBF；
（2）由AB=CB，∠ABC=90°，即可求得∠CAB与∠ACB的度数，即可得∠BAE的度数，又由Rt△ABE≌Rt△CBF，即可求得∠BCF的度数，则由∠ACF=∠BCF+∠ACB即可求得答案．
（1）证明：∵∠ABC=90°，... 如图所示，在Rt△ACD和Rt△BCE中，若AD＝BE，DC＝EC，则无法得出的结论是( )
A. OA＝OB B. E是AC的中点 C. △AOE≌△BOD D. AE＝BD
B
【解析】∵∠C=∠C=90°，
∴△ACD和△BCE是直角三角形，
在Rt△ACD和Rt△BCE中，
∴Rt△ACD≌Rt△BCE（HL），
∴∠B=∠A，CB=CA，
∵CD=CE，
∴AE=BD，故D正确，
在△AOE和△BOD中，
∴△AOE≌△BOD（AAS），故C正确，
∴AO=OB，故A正确，
AE=BD，CE=CD... 如图，将以A为直角顶点的等腰Rt△ABC沿直线BC平移得到△A′B′C′，使点B′与C重合，连接A′B，则sin∠A′BC′的值为_____，cos∠A′BC＝________．
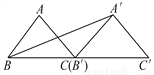
【解析】过A′作出A′D⊥BC′，垂足为D，
在等腰直角三角形A′B′C′中，则A′D是底边上的中线，
∴B′C′=2 A′D，
∵BC=B′C′，BD=BC+B′D，
∴A′B= ，
∴ sin∠A′BC′=，cos∠A′BC＝，
故答案为： ， . 如图，在Rt△ABC中，∠ACB＝90°，D是AB的中点，过D点作AB的垂线交AC于点E，BC＝6，sinA＝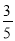
，则DE＝____________．
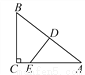
【解析】试题分析：在Rt△ABC中，先求出AB，AC继而得出AD，再由△ADE∽△ACB，利用对应边成比例可求出DE．
试题解析：∵BC=6，sinA=，
∴AB=10，
∴AC=，
∵D是AB的中点，
∴AD=AB=5，
∵△ADE∽△ACB，
∴，即，
解得：DE=．
考点: 1.解直角三角形；2.线段垂直平分线的性质；3勾股定理.
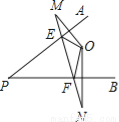
... 如图所示，已知O是∠APB内的一点，点M，N分别是O点关于PA，PB的对称点，MN与PA，PB分别相交于点E，F，已知MN=5cm，则△OEF的周长为 .
5cm．
【解析】
试题分析： ∵O是∠APB内的一点，点M，N分别是O点关于PA，PB的对称点，∴OE=ME，OF=NF，
∵MN=5cm，∴△OEF的周长为：OE+EF+OF=ME+EF+NF=MN=5（cm）．故答案为：5cm．