题目内容
下列各组条件中,能判断两个直角三角形全等的是( )
A. 一组边对应相等 B. 两组直角边对应相等
C. 两组锐角对应相等 D. 一组锐角对应相等
 B
【解析】A、两直角三角形隐含一个条件是两直角相等,现已知一组边对应相等 ,要判定两直角三角形全等,还需要一组角对应相等地或是另一组边对应相等才能进行判定,故选项错误;
B、可以利用边角边判定两三角形全等,故本选项正确;
C、两个锐角分别相等,只有角没有边,不能判定全等,此选项错误;
D、一组锐角对应相等,隐含一个条件是两直角相等,根据角对应相等,不能判定三角形全等,故选...
B
【解析】A、两直角三角形隐含一个条件是两直角相等,现已知一组边对应相等 ,要判定两直角三角形全等,还需要一组角对应相等地或是另一组边对应相等才能进行判定,故选项错误;
B、可以利用边角边判定两三角形全等,故本选项正确;
C、两个锐角分别相等,只有角没有边,不能判定全等,此选项错误;
D、一组锐角对应相等,隐含一个条件是两直角相等,根据角对应相等,不能判定三角形全等,故选...
练习册系列答案
相关题目
如下图所示,判断各组中的两个图形是否是全等图形.
A. 
B. 
C. 
D. 
 A
【解析】全等图形需要大小相等,形状相同,原图中只有A同时符合这两个条件,B、C、D都只是形状相同,但大小不相等,
故选A.
A
【解析】全等图形需要大小相等,形状相同,原图中只有A同时符合这两个条件,B、C、D都只是形状相同,但大小不相等,
故选A. 在下列长度的四根木棒中,能与4cm、9cm长的两根木棒钉成一个三角形的是( )
A. 4cm B. 5cm C. 9cm D. 13cm
 C
【解析】试题解析:根据三角形的三边关系,得:第三边应大于两边之差,且小于两边之和,
即9-4=5,9+4=13.
∴第三边取值范围应该为:5<第三边长度<13,
故只有C选项符合条件.
故选C.
C
【解析】试题解析:根据三角形的三边关系,得:第三边应大于两边之差,且小于两边之和,
即9-4=5,9+4=13.
∴第三边取值范围应该为:5<第三边长度<13,
故只有C选项符合条件.
故选C. (2011•江津区)在△ABC中,AB=CB,∠ABC=90°,F为AB延长线上一点,点E在BC上,且AE=CF.
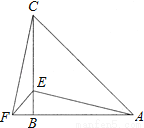
(1)求证:Rt△ABE≌Rt△CBF;
(2)若∠CAE=30°,求∠ACF的度数.
 (1)见解析;(2)60°.
【解析】
试题分析:(1)由AB=CB,∠ABC=90°,AE=CF,即可利用HL证得Rt△ABE≌Rt△CBF;
(2)由AB=CB,∠ABC=90°,即可求得∠CAB与∠ACB的度数,即可得∠BAE的度数,又由Rt△ABE≌Rt△CBF,即可求得∠BCF的度数,则由∠ACF=∠BCF+∠ACB即可求得答案.
(1)证明:∵∠ABC=90°,...
(1)见解析;(2)60°.
【解析】
试题分析:(1)由AB=CB,∠ABC=90°,AE=CF,即可利用HL证得Rt△ABE≌Rt△CBF;
(2)由AB=CB,∠ABC=90°,即可求得∠CAB与∠ACB的度数,即可得∠BAE的度数,又由Rt△ABE≌Rt△CBF,即可求得∠BCF的度数,则由∠ACF=∠BCF+∠ACB即可求得答案.
(1)证明:∵∠ABC=90°,... 如图,有一个直角△ABC,∠C=90°,AC=10,BC=5,一条线段PQ=AB,P.Q两点分别在AC和过点A且垂直于AC的射线AX上运动,当AP= 时,才能使ΔABC≌ΔPQA.
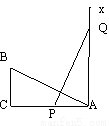
 10
【解析】
试题分析:要使△ABC≌△PQA,根据全等三角形的性质可得AP=CA,则说明当P运动到C时,利用直角三角形全等的判定HL可证△ABC≌△PQA.
∵AX⊥AC,∠C=90°,
∴∠C=∠PAQ=90°,
又∵AP=CB=5,PQ=AB,
∴△ABC≌△PQA.
点P运动到C点时,△ABC≌△PQA.
∵AX⊥AC,∠C=90°,
...
10
【解析】
试题分析:要使△ABC≌△PQA,根据全等三角形的性质可得AP=CA,则说明当P运动到C时,利用直角三角形全等的判定HL可证△ABC≌△PQA.
∵AX⊥AC,∠C=90°,
∴∠C=∠PAQ=90°,
又∵AP=CB=5,PQ=AB,
∴△ABC≌△PQA.
点P运动到C点时,△ABC≌△PQA.
∵AX⊥AC,∠C=90°,
... 如图,将以A为直角顶点的等腰Rt△ABC沿直线BC平移得到△A′B′C′,使点B′与C重合,连接A′B,则sin∠A′BC′的值为_____,cos∠A′BC=________.
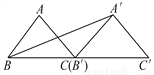
 【解析】过A′作出A′D⊥BC′,垂足为D,
在等腰直角三角形A′B′C′中,则A′D是底边上的中线,
∴B′C′=2 A′D,
∵BC=B′C′,BD=BC+B′D,
∴A′B= ,
∴ sin∠A′BC′=,cos∠A′BC=,
故答案为: , .
【解析】过A′作出A′D⊥BC′,垂足为D,
在等腰直角三角形A′B′C′中,则A′D是底边上的中线,
∴B′C′=2 A′D,
∵BC=B′C′,BD=BC+B′D,
∴A′B= ,
∴ sin∠A′BC′=,cos∠A′BC=,
故答案为: , . 如图,在Rt△ABC中,∠C=90°,若sinA=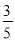 ,则cosB的是
,则cosB的是
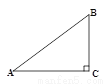
A. 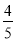 B.
B. 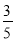 C.
C. 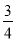 D.
D. 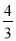
 B
【解析】试题分析:在Rt△ABC中,∵∠C=90°,
∴∠A+∠B=90°,
∴cosB=sinA,
∵sinA=,
∴cosB=.
故选:B.
B
【解析】试题分析:在Rt△ABC中,∵∠C=90°,
∴∠A+∠B=90°,
∴cosB=sinA,
∵sinA=,
∴cosB=.
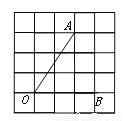
故选:B. 如图,将∠AOB放置在5×5的正方形网格中,则sin∠AOB的值是( )
A.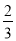 B.
B.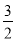 C.
C.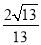 D.
D.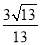
 D.
【解析】
试题分析:在直角△OAC中,OC=2,AC=3,则OA===,则sin∠AOB===.故选D.
D.
【解析】
试题分析:在直角△OAC中,OC=2,AC=3,则OA===,则sin∠AOB===.故选D. 如图是经过轴对称变换后所得的图形,与原图形相比
A.形状没有改变,大小没有改变 B.形状没有改变,大小有改变
C.形状有改变,大小没有改变 D.形状有改变,大小有改变
 A
【解析】
试题分析:∵轴对称变换不改变图形的形状与大小,
∴与原图形相比,形状没有改变,大小没有改变。
故选A。
A
【解析】
试题分析:∵轴对称变换不改变图形的形状与大小,
∴与原图形相比,形状没有改变,大小没有改变。
故选A。 
