1.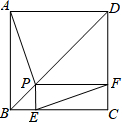 如图,P为边长为2的正方形ABCD的对角线BD上任一点,过点P作PE⊥BC于点E,PF⊥CD于点F,连接EF.给出以下4个结论:①AP=EF;②AP⊥EF;③EF最短长度为$\sqrt{2}$;④若∠BAP=30°时,则EF的长度为2.其中结论正确的有( )
如图,P为边长为2的正方形ABCD的对角线BD上任一点,过点P作PE⊥BC于点E,PF⊥CD于点F,连接EF.给出以下4个结论:①AP=EF;②AP⊥EF;③EF最短长度为$\sqrt{2}$;④若∠BAP=30°时,则EF的长度为2.其中结论正确的有( )
 如图,P为边长为2的正方形ABCD的对角线BD上任一点,过点P作PE⊥BC于点E,PF⊥CD于点F,连接EF.给出以下4个结论:①AP=EF;②AP⊥EF;③EF最短长度为$\sqrt{2}$;④若∠BAP=30°时,则EF的长度为2.其中结论正确的有( )
如图,P为边长为2的正方形ABCD的对角线BD上任一点,过点P作PE⊥BC于点E,PF⊥CD于点F,连接EF.给出以下4个结论:①AP=EF;②AP⊥EF;③EF最短长度为$\sqrt{2}$;④若∠BAP=30°时,则EF的长度为2.其中结论正确的有( )| A. | ①②③ | B. | ①②④ | C. | ②③④ | D. | ①③④ |
19.某服装店公布以下好消息:为了感谢广大顾客的支持,即日起,在我店办会员卡同时享受以下两种优惠:
优惠一:
优惠二:
注:1-100是指购买服装的标价大于或等于1元且小于100元,其他类同.
若该店服装的标价都是正整数,请解决以下问题:
(1)在该店公布好消息的前、后,如果顾客都是充值1000元,在所买服装打折后的价格不超过会员卡内金额的前提下,可买到最贵的服装的标价相差了多少元?
(2)小红和小亮都在该店公布好消息之后办了会员卡,两人各买了一件标价高于300元的服装,小亮所买服装的标价比小红的高,但比较打折后的价格,小亮的低,求小亮买的服装的标价的范围.
优惠一:
| 充值金额(元) | 充值后卡内金额(元) | |
| 以前 | 即日起 | |
| 200 | 200 | 250 |
| 500 | 600 | 650 |
| 1000 | 1200 | 1400 |
| 购买服装的标价(元) | 折扣 | |
| 以前 | 即日起 | |
| 1-100 | 不打折 | 不打折 |
| 100-300 | 不打折 | 9折 |
| 300-400 | 9折 | 8折 |
| 不低于400 | 8折 | 7折 |
若该店服装的标价都是正整数,请解决以下问题:
(1)在该店公布好消息的前、后,如果顾客都是充值1000元,在所买服装打折后的价格不超过会员卡内金额的前提下,可买到最贵的服装的标价相差了多少元?
(2)小红和小亮都在该店公布好消息之后办了会员卡,两人各买了一件标价高于300元的服装,小亮所买服装的标价比小红的高,但比较打折后的价格,小亮的低,求小亮买的服装的标价的范围.
18.(1)问题背景
如图甲,∠ADC=∠B=90°,DE⊥AB,垂足为E,且AD=CD,DE=5,求四边形ABCD的面积.

请直接写出四边形ABCD的面积为25.
(2)类比迁移
如图乙,P为等边△ABC外一点,BP=1,CP=3,且∠BPC=120°,求四边形ABPC的面积.
(3)拓展延伸
如图丙,在五边形ABCDE中,BC=4,CD+AB=4,AE=DE=6,AE⊥AB,DE⊥CD,求五边形ABCDE的面积.
0 297555 297563 297569 297573 297579 297581 297585 297591 297593 297599 297605 297609 297611 297615 297621 297623 297629 297633 297635 297639 297641 297645 297647 297649 297650 297651 297653 297654 297655 297657 297659 297663 297665 297669 297671 297675 297681 297683 297689 297693 297695 297699 297705 297711 297713 297719 297723 297725 297731 297735 297741 297749 366461
如图甲,∠ADC=∠B=90°,DE⊥AB,垂足为E,且AD=CD,DE=5,求四边形ABCD的面积.

小明发现四边形ABCD的一组领边AD=CD,这就为旋转作了铺垫.于是,小明同学有如下思考过程: 第一步:将△ADE绕点D逆时针旋转90°; 第二步:利用∠A与∠DCB互补, 证明F、C、B三点共线, 从而得到正方形DEBF; 进而求得四边形ABCD的面积. 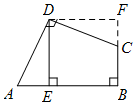 |
(2)类比迁移
如图乙,P为等边△ABC外一点,BP=1,CP=3,且∠BPC=120°,求四边形ABPC的面积.
(3)拓展延伸
如图丙,在五边形ABCDE中,BC=4,CD+AB=4,AE=DE=6,AE⊥AB,DE⊥CD,求五边形ABCDE的面积.
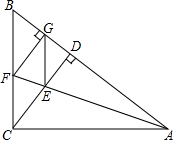 如图,在Rt△ABC中,∠ACB=90°,CD为AB边上的高,∠CAB的平分线交CD于点E,交CB于点F,过点F作FG⊥AB于点G,连接GE.求证:四边形CEGF是菱形.
如图,在Rt△ABC中,∠ACB=90°,CD为AB边上的高,∠CAB的平分线交CD于点E,交CB于点F,过点F作FG⊥AB于点G,连接GE.求证:四边形CEGF是菱形.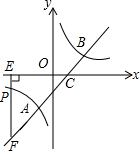 如图,直线y=x-1与反比例函数y=$\frac{k}{x}$的图象交于A,B两点,与x轴交于点C,已知点A的横坐标为-1.
如图,直线y=x-1与反比例函数y=$\frac{k}{x}$的图象交于A,B两点,与x轴交于点C,已知点A的横坐标为-1.