题目内容
18.(1)问题背景如图甲,∠ADC=∠B=90°,DE⊥AB,垂足为E,且AD=CD,DE=5,求四边形ABCD的面积.

小明发现四边形ABCD的一组领边AD=CD,这就为旋转作了铺垫.于是,小明同学有如下思考过程: 第一步:将△ADE绕点D逆时针旋转90°; 第二步:利用∠A与∠DCB互补, 证明F、C、B三点共线, 从而得到正方形DEBF; 进而求得四边形ABCD的面积. 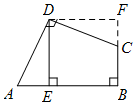 |
(2)类比迁移
如图乙,P为等边△ABC外一点,BP=1,CP=3,且∠BPC=120°,求四边形ABPC的面积.
(3)拓展延伸
如图丙,在五边形ABCDE中,BC=4,CD+AB=4,AE=DE=6,AE⊥AB,DE⊥CD,求五边形ABCDE的面积.
分析 (1)根据四边形ABCD的面积等于正方形EBFD的面积计算即可;
(2)如图乙中,延长PC至D,取CD=1,连接AD.只要证明△ABP≌△ACD(SAS),即可推出四边形ABPC的面积等于△APD的面积;
(3)如图丙中,延长CD至DF=AB,连接EF、BE、CE.只要证明五边形ABCDE的面积等于四边形BCFE的面积即可;
解答 解:(1)由题可知${S_{四边形ABCD}}={S_{正方形DEBF}}={5^2}=25$.
故答案为25.
(2)如图,延长PC至D,取CD=1,连接AD.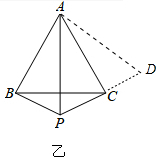
∵等边△ABC中,∠BAC=60°.
∵∠BOC=120°,
∴∠BPC=120°,
∴∠BPC+∠BAC=180°,
∴四边形ABPC中,∠ABP+∠ACP=360°-180°=180°,
∴∠ABP=∠ACD=180°-∠ACP,
又∵AB=AC,BP=CD,
∴△ABP≌△ACD(SAS),
∴AP=AP,∠BAP=∠CAP.
∵∠BAP+∠PAC=∠BAC=60°,
∴∠CAD+∠PAC=60°,
∴△APD为等边三角形且PD=PC+CD=3+1=4,
∴${S_{四边形ABPC}}={S_{△ADP}}=\frac{{\sqrt{3}}}{4}×{4^2}=4\sqrt{3}$.
(3)如图,延长CD至DF=AB,连接EF、BE、CE.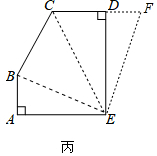
∵AB=DF,AE=DE,∠BAE=∠FDE=90°,
∴△ABE≌△DFE(SAS),
∴EB=EF.
∵CD+AB=CD+DF=4,BC=4,
∴CD+DF=CF=BC,
∴△EBC≌△EFC(SSS),
∴${S_{五边形ABCDE}}={S_{四边形BCFE}}=2{S_{△ECF}}=2×\frac{1}{2}×4×6=24$.
点评 本题考查四边形综合题、旋转变换、全等三角形的判定和性质、等边三角形的性质等知识,解题的关键是灵活运用所学知识解决问题,学会利用旋转法添加辅助线,构造全等三角形解决问题,属于中考压轴题.

| 厂家 | 超过标准质量的部分 | |||||
| 甲 | -3 | 0 | 0 | 1 | 2 | 0 |
| 乙 | -2 | 1 | -1 | 0 | 1 | 1 |
(2)通过计算,你认为哪一家生产皮具的质量比较稳定?
| A. | -1 | B. | 0 | C. | 1 | D. | 2 |
| 级数 | 全月应纳税所得额 | 税率% |
| 1 | 不超过500元的部分 | 5 |
| 2 | 超过500元至2000元的部分 | 10 |
| 3 | 超过2000元至5000元的部分 | 15 |
| 4 | 超过5000元至20000元的部分 | 20 |
| … | … |
| 公民 | 工资薪金(元) | 应纳税金(元) |
| 甲 | 2000 | 0 |
| 乙 | 2500 | 25 |
| 丙 | 3900 | 165 |
| A. | $\sqrt{x+1}+\sqrt{x+2}+3=0$ | B. | $\sqrt{x-9}+\sqrt{4-x}=16$ | ||
| C. | $\sqrt{{x}^{2}+1}-\sqrt{{x}^{2}+2}=1-\frac{1}{\sqrt{{x}^{2}+1}}$ | D. | 6$\sqrt{{x}^{2}-2x+6}=21+2x-{x}^{2}$ |
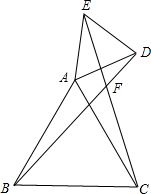 已知:如图所示,△ABC与△ADE均为等边三角形,点A为它们公共顶点,现连接BD、EC,BD与EC交于F点:
已知:如图所示,△ABC与△ADE均为等边三角形,点A为它们公共顶点,现连接BD、EC,BD与EC交于F点: