题目内容
15.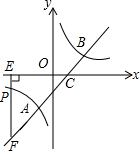 如图,直线y=x-1与反比例函数y=$\frac{k}{x}$的图象交于A,B两点,与x轴交于点C,已知点A的横坐标为-1.
如图,直线y=x-1与反比例函数y=$\frac{k}{x}$的图象交于A,B两点,与x轴交于点C,已知点A的横坐标为-1.(1)求反比例函数的解析式;
(2)若点P是反比例函数图象上一点,过点P作PE⊥x轴于点E,延长EP交直线AB于点F,若CF=3BC,求点P的坐标和△CEF的面积.
分析 (1)把点A的横坐标代入一次函数解析式,求出点A的坐标.由于点A在反比例函数图象上,利用待定系数法求出反比例函数解析式.
(2)由于点A、B是一次函数与反比例函数的交点,可求出交点B的坐标.过B做BD⊥x轴垂足为D.易得△BCD∽△FCE,由CF=3BC,易求出点F的纵坐标及F点的坐标.因为点F与点P横坐标相同,可求出P点的坐标.求出CE、EF后再计算出△CEF的面积.
解答 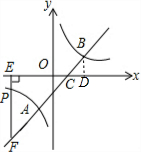 解:(1)将点A的横坐标x=-1代入y=x-1,可得y=-1-1=-2.
解:(1)将点A的横坐标x=-1代入y=x-1,可得y=-1-1=-2.
∴A(-1,-2).
将点A(-1.-2)代入反比例函数y=$\frac{k}{x}$,得k=-1×(-2)=2.
∴反比例函数解析式为:y=$\frac{2}{x}$.
(2)过B作BD⊥x轴于点D,则BD∥EF,
∴△EFC∽△DBC,
∴$\frac{EF}{BD}=\frac{EC}{CD}=\frac{CF}{BC}$=3,
由$\frac{2}{x}$=x-1得:x1=-1,x2=2,
∵B在第一象限,
∴点B的横坐标为2,
把x=2代入y=x-1中得:y=1,
∴B(2,1),
∴BD=1,
∴EF=3BD=3,
∴点F的纵坐标为-3,
把y=-3代入y=x-1中得:x=-2,
∴F(-2,-3),
将x=-2代入y=$\frac{2}{x}$中得:y=-1,
∴P(-2,-1),
y=0时,x-1=0,x=1,
∴OC=1,
∵EF=3,CE=OE+OC=2+1=3,
∴S△CEF=$\frac{1}{2}$CE×EF=$\frac{1}{2}$×3×3=$\frac{9}{2}$.
点评 本题考查了反比例函数和一次函数的交点问题、利用待定系数法求函数的解析式、与坐标轴的交点、三角形相似的性质和判定,属于基础题,熟练掌握图形与坐标特点是关键.

 阳光同学一线名师全优好卷系列答案
阳光同学一线名师全优好卷系列答案| A. | 0 | B. | 1 | C. | -1 | D. | 1或-1 |
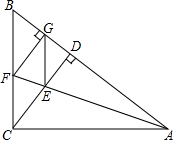 如图,在Rt△ABC中,∠ACB=90°,CD为AB边上的高,∠CAB的平分线交CD于点E,交CB于点F,过点F作FG⊥AB于点G,连接GE.求证:四边形CEGF是菱形.
如图,在Rt△ABC中,∠ACB=90°,CD为AB边上的高,∠CAB的平分线交CD于点E,交CB于点F,过点F作FG⊥AB于点G,连接GE.求证:四边形CEGF是菱形.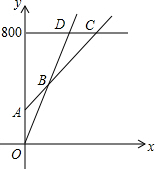 某市游泳馆为了满足不同顾客的需求,设计了三种游泳票:普通票价每次20元/张;金卡售价800元/张,每次凭卡不再收费;银卡售价200元/张,每次凭卡另收10元.这样顾客可根据游泳次数的多少选择不同的消费方式.普通票全年正常出售,两种优惠卡仅限暑期使用,不限次数.设游泳x次时,所需总费用为y元.
某市游泳馆为了满足不同顾客的需求,设计了三种游泳票:普通票价每次20元/张;金卡售价800元/张,每次凭卡不再收费;银卡售价200元/张,每次凭卡另收10元.这样顾客可根据游泳次数的多少选择不同的消费方式.普通票全年正常出售,两种优惠卡仅限暑期使用,不限次数.设游泳x次时,所需总费用为y元.