题目内容
20.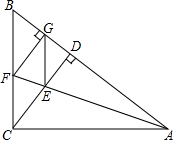 如图,在Rt△ABC中,∠ACB=90°,CD为AB边上的高,∠CAB的平分线交CD于点E,交CB于点F,过点F作FG⊥AB于点G,连接GE.求证:四边形CEGF是菱形.
如图,在Rt△ABC中,∠ACB=90°,CD为AB边上的高,∠CAB的平分线交CD于点E,交CB于点F,过点F作FG⊥AB于点G,连接GE.求证:四边形CEGF是菱形.
分析 由角平分线的性质得出CF=GF,∠CAF=∠BAF,证出CD∥GF,由角的互余关系和对顶角相等得出∠CFE=∠AED=∠CEF,证出CE=CF,得出CE=GF,证出四边形CEGF是平行四边形,即可证出四边形CEGF是菱形.
解答 证明:∵AF平分∠BAC,∠ACB=90°,FG⊥AB于点G,
∴CF=GF,∠CAF=∠BAF,
∵CD⊥AB,
∴CD∥GF,
∵∠CFE+∠CAF=90°,∠AED+∠BAF=90°,
∴∠CFE=∠AED=∠CEF,
∴CE=CF,
∴CE=GF,
∴四边形CEGF是平行四边形,
又∵CE=CF,
∴四边形CEGF是菱形.
点评 本题考查了角平分线的定义、等腰三角形的判定与性质、平行四边形的判定、菱形的判定;本题有一定难度,证明三角形是等腰三角形是解决问题的关键.

练习册系列答案
 浙江之星学业水平测试系列答案
浙江之星学业水平测试系列答案 高效智能课时作业系列答案
高效智能课时作业系列答案
相关题目
6.$\frac{2}{5}:{0}.{6}$化为最简整数比是( )
| A. | 2:3 | B. | 8:5 | C. | 10:1 | D. | 5:8 |
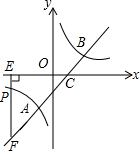 如图,直线y=x-1与反比例函数y=$\frac{k}{x}$的图象交于A,B两点,与x轴交于点C,已知点A的横坐标为-1.
如图,直线y=x-1与反比例函数y=$\frac{k}{x}$的图象交于A,B两点,与x轴交于点C,已知点A的横坐标为-1.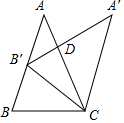 如图,在△ABC中,AB=AC,将△ABC绕点C顺时针旋转后得到△A'B'C,设∠A'CB=a,点B'在AB上,则∠ADA'=4α-360°(用含a的式子表示)
如图,在△ABC中,AB=AC,将△ABC绕点C顺时针旋转后得到△A'B'C,设∠A'CB=a,点B'在AB上,则∠ADA'=4α-360°(用含a的式子表示)