12.我们已经学习了利用配方法解一元二次方程,其实配方法还有其它重要应用.
例:已知x可取任何实数,试求二次三项式2x2-12x+14的值的范围.
解:2x2-12x+14=2(x2-6x)+14=2(x2-6x+32-32)+14
=2[(x-3)2-9]+14=2(x-3)2-18+14=2(x-3)2-4.
∵无论x取何实数,总有(x-3)2≥0,∴2(x-3)2-4≥-4.
即无论x取何实数,2x2-12x+14的值总是不小于-4的实数.
问题:已知x可取任何实数,则二次三项式-3x2+12x-11的最值情况是( )
例:已知x可取任何实数,试求二次三项式2x2-12x+14的值的范围.
解:2x2-12x+14=2(x2-6x)+14=2(x2-6x+32-32)+14
=2[(x-3)2-9]+14=2(x-3)2-18+14=2(x-3)2-4.
∵无论x取何实数,总有(x-3)2≥0,∴2(x-3)2-4≥-4.
即无论x取何实数,2x2-12x+14的值总是不小于-4的实数.
问题:已知x可取任何实数,则二次三项式-3x2+12x-11的最值情况是( )
| A. | 有最大值-1 | B. | 有最小值-1 | C. | 有最大值1 | D. | 有最小值1 |
11.若关于x的一元二次方程x2-4x-k=0有两个实数根,则( )
0 283768 283776 283782 283786 283792 283794 283798 283804 283806 283812 283818 283822 283824 283828 283834 283836 283842 283846 283848 283852 283854 283858 283860 283862 283863 283864 283866 283867 283868 283870 283872 283876 283878 283882 283884 283888 283894 283896 283902 283906 283908 283912 283918 283924 283926 283932 283936 283938 283944 283948 283954 283962 366461
| A. | k>4 | B. | k>-4 | C. | k≥4 | D. | k≥-4 |
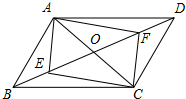 如图,在?ABCD中,AC与BD交于点O,点E,F都在BD上,BE=DF.
如图,在?ABCD中,AC与BD交于点O,点E,F都在BD上,BE=DF.