题目内容
11.若关于x的一元二次方程x2-4x-k=0有两个实数根,则( )| A. | k>4 | B. | k>-4 | C. | k≥4 | D. | k≥-4 |
分析 根据关于x的一元二次方程x2-4x-k=0有两个实数根,得出△=(-4)2-4×1×(-k)≥0,从而求出k的取值范围.
解答 解:∵一元二次方程x2-4x-k=0有两个实数根,
∴△=(-4)2-4×1×(-k)≥0,
即:16+4k≥0,
解得:k≥-4,
故选:D.
点评 此题主要考查了一元二次方程根的情况与判别式,关键是掌握一元二次方程根的情况与判别式△的关系:
(1)△>0?方程有两个不相等的实数根;
(2)△=0?方程有两个相等的实数根;
(3)△<0?方程没有实数根.

练习册系列答案
相关题目
1. 如图,已知AB∥CD,HL∥FG,EF⊥CD,∠1=50°,那么,∠EHL的度数为( )
如图,已知AB∥CD,HL∥FG,EF⊥CD,∠1=50°,那么,∠EHL的度数为( )
 如图,已知AB∥CD,HL∥FG,EF⊥CD,∠1=50°,那么,∠EHL的度数为( )
如图,已知AB∥CD,HL∥FG,EF⊥CD,∠1=50°,那么,∠EHL的度数为( )| A. | 40° | B. | 45° | C. | 50° | D. | 55° |
19.若二次根式$\frac{\sqrt{x+1}}{2}$在实数范围内有意义,则x的取值范围是( )
| A. | x≥-1 | B. | x≠2 | C. | x≥-1且x≠2 | D. | 以上都不正确 |
3. 如图,若在象棋棋盘上建立平面直角坐标系,使“帅”位于点(-1,-2),“马”位于点(2,-2),则“兵”位于点( )
如图,若在象棋棋盘上建立平面直角坐标系,使“帅”位于点(-1,-2),“马”位于点(2,-2),则“兵”位于点( )
 如图,若在象棋棋盘上建立平面直角坐标系,使“帅”位于点(-1,-2),“马”位于点(2,-2),则“兵”位于点( )
如图,若在象棋棋盘上建立平面直角坐标系,使“帅”位于点(-1,-2),“马”位于点(2,-2),则“兵”位于点( )| A. | (-1,1) | B. | (-2,-1) | C. | (-3,1) | D. | (1,-2) |
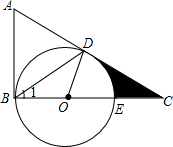 如图,在△ABC=90°,D是边AC上的一点,连接BD,使∠A=2∠1,E是BC上的一点,以BE为直径的⊙O经过点D.
如图,在△ABC=90°,D是边AC上的一点,连接BD,使∠A=2∠1,E是BC上的一点,以BE为直径的⊙O经过点D.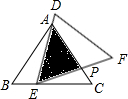 如图,在△ABC中,已知AB=AC=6,BC=8,且△ABC≌△DEF,将△DEF与△ABC重合在一起,△ABC不动,△DEF运动,并满足:点E在边BC上沿B到C的方向运动,且DE始终经过点A,EF与AC交于P点.
如图,在△ABC中,已知AB=AC=6,BC=8,且△ABC≌△DEF,将△DEF与△ABC重合在一起,△ABC不动,△DEF运动,并满足:点E在边BC上沿B到C的方向运动,且DE始终经过点A,EF与AC交于P点.