Question

20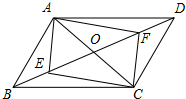．如图，在?ABCD中，AC与BD交于点O，点E，F都在BD上，BE=DF．
（1）求证：四边形AECF是平行四边形．
（2）若AB⊥AC，AB=4，AC=6，当?AECF是矩形时，求BE的长．

Answer 1

分析 （1）由平行四边形的性质得出OA=OC，OB=OD，证出OE=OF，即可得出四边形AECF是平行四边形．
（2）求出OA=$\frac{1}{2}$AC=3，由勾股定理求出OB，由矩形的性质得出OE=OA=3，即可得出结果．

解答 （1）证明：∵四边形ABCD是平行四边形，
∴OA=OC，OB=OD，
∵BE=DF，
∴OE=OF，
∴四边形AECF是平行四边形．
（2）解：∵OA=$\frac{1}{2}$AC=3，AB⊥AC，
∴OB=$\sqrt{A{B}^{2}+O{A}^{2}}$=$\sqrt{{4}^{2}+{3}^{2}}$=5，
当?AECF是矩形时，OE=OA=3，
∴BE=OB-OE=5-3=2．

点评 本题考查了平行四边形的判定与性质、勾股定理、矩形的性质；熟练掌握平行四边形的判定与性质，由勾股定理求出OB是解决问题（2）的关键．．