题目内容
13.若二次根式$\sqrt{3-x}$有意义,则x的取值范围是x≤3.分析 直接利用二次根式的性质得出3-x的取值范围,进而求出答案.
解答 解:∵二次根式$\sqrt{3-x}$有意义,
∴3-x≥0,
解得:x≤3.
故答案为:x≤3.
点评 此题主要考查了二次根式有意义的条件,正确把握二次根式的性质是解题关键.

练习册系列答案
相关题目
4. 如图,将长方体表面展开,下列选项中错误的是( )
如图,将长方体表面展开,下列选项中错误的是( )
 如图,将长方体表面展开,下列选项中错误的是( )
如图,将长方体表面展开,下列选项中错误的是( )| A. |  | B. |  | C. |  | D. |  |
1.方程x2+4x-$\frac{10}{x}$+1=0的正数根的取值范围是( )
| A. | 0<x<1 | B. | 1<x<2 | C. | 2<x<3 | D. | 3<x<4 |
8.在下列各式中,计算正确的是( )
| A. | (2$\sqrt{3}$)2=6 | B. | $\sqrt{9}$=±3 | C. | $\sqrt{(-6)^2}$=-6 | D. | $\frac{1}{2+\sqrt{3}}$=2-$\sqrt{3}$ |
3.若|a-b+1|与$\sqrt{a+2b+4}$互为相反数,则(a+b)2的值是( )
| A. | 25 | B. | 16 | C. | 9 | D. | 4 |
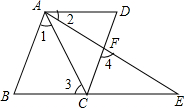 已知:如图,AB∥CD,∠1=∠2,∠3=∠4.
已知:如图,AB∥CD,∠1=∠2,∠3=∠4.