9、解:(1)由已知可设M(-c,y),
则有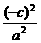 +
+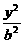 =1.
=1.
∵M在第二象限,∴M(-c,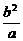 ).
).
又由AB∥OM,可知kAB=kOM.
∴-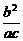 =-
=-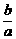 .∴b=c.∴a=
.∴b=c.∴a=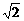 b.
b.
∴e=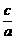 =
=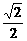 .
.
(2)设|F1Q|=m,|F2Q|=n,
则m+n=2a,mn>0.|F1F2|=2c,a2=2c2,
∴cos∠F1QF2=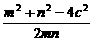
=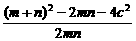 =
=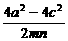 -1
-1
=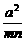 -1≥
-1≥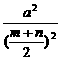 -1=
-1=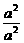 -1=0.
-1=0.
当且仅当m=n=a时,等号成立.
故∠F1QF2∈[0,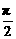 ].
].
(3)∵CD∥AB,kCD=-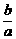 =-
=-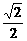 .
.
设直线CD的方程为y=-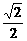 (x+c),
(x+c),
即y=-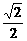 (x+b).
(x+b).
|
|
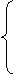
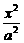 +
+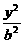 =1,
=1,
y=-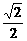 (x+b).
(x+b).
(a2+2b2)x2+2a2bx-a2b2=0.
设C(x1,y1)、D(x2,y2),∵a2=2b2,
∴x1+x2=-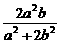 =-
=-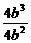 =-b,
=-b,
x1·x2=-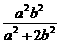 =-
=-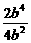 =-
=-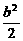 .
.
∴|CD|=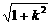 |x1-x2|
|x1-x2|
=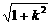 ·
·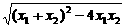
=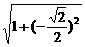 ·
·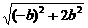 =
=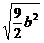 =3.
=3.
∴b2=2,则a2=4.
∴椭圆的方程为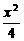 +
+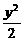 =1.
=1.
 (1)设P点的坐标为(x1,y1),则Q点坐标为(x1,-y1),又有A1(-m,0),A2(m,0),则A1P的方程为
(1)设P点的坐标为(x1,y1),则Q点坐标为(x1,-y1),又有A1(-m,0),A2(m,0),则A1P的方程为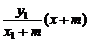 ①
①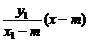 ②
②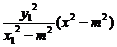 ③
③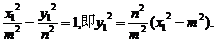
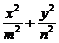 =1
=1 此即为M的轨迹方程
此即为M的轨迹方程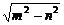 ,0),准线方程为x=±
,0),准线方程为x=±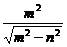 ,离心率e=
,离心率e=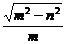 ;
;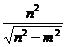 ,离心率e=
,离心率e=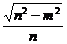
 解
解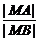 =λ,坐标代入,得
=λ,坐标代入,得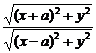 =λ,化简得
=λ,化简得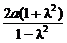 x+a2=0
x+a2=0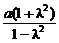 ,0)为圆心,
,0)为圆心,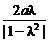 为半径的圆
为半径的圆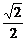 ,可设椭圆方程为
,可设椭圆方程为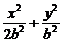 =1,
=1,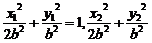 =1,两式相减,得
=1,两式相减,得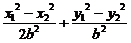 =0,
=0,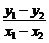 =-1,故直线AB的方程为y=-x+3,
=-1,故直线AB的方程为y=-x+3,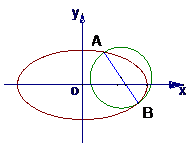 又|AB|=
又|AB|=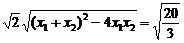 ,
,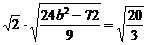 ,解得b2=8
,解得b2=8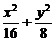 =1
=1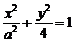 ①
①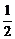 (x1+x2)=
(x1+x2)=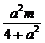 ,y0=-x0+m=
,y0=-x0+m=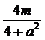
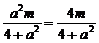 ,
,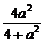 ,
,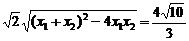 ,
,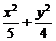 =1
=1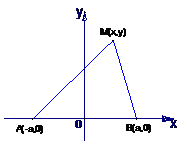 已知A、B为两定点,动点M到A与到B的距离比为常数λ,求点M的轨迹方程,并注明轨迹是什么曲线
已知A、B为两定点,动点M到A与到B的距离比为常数λ,求点M的轨迹方程,并注明轨迹是什么曲线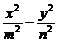 =1(m>0,n>0)的顶点为A1、A2,与y轴平行的直线l交双曲线于点P、Q .
=1(m>0,n>0)的顶点为A1、A2,与y轴平行的直线l交双曲线于点P、Q . 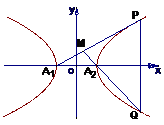 (2)当m≠n时,求所得圆锥曲线的焦点坐标、准线方程和离心率
(2)当m≠n时,求所得圆锥曲线的焦点坐标、准线方程和离心率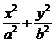 =1(a>b>0) ,点P为其上一点,F1、F2为椭圆的焦点,∠F1PF2的外角平分线为l,点F2关于l的对称点为Q,F2Q交l于点R .
=1(a>b>0) ,点P为其上一点,F1、F2为椭圆的焦点,∠F1PF2的外角平分线为l,点F2关于l的对称点为Q,F2Q交l于点R . 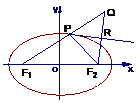 (2)设点R形成的曲线为C,直线l:y=k(x+
(2)设点R形成的曲线为C,直线l:y=k(x+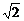 a)与曲线C相交于A、B两点,当△AOB的面积取得最大值时,求k的值
a)与曲线C相交于A、B两点,当△AOB的面积取得最大值时,求k的值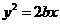 )D 2、D
3、
)D 2、D
3、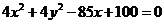 4、
4、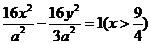
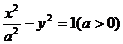 的一条准线与抛物线
的一条准线与抛物线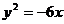 的准线重合,则该双曲线的离心率为
( )
的准线重合,则该双曲线的离心率为
( )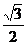 B.
B.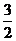 C.
C.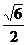 D.
D.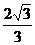
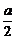 ,0),C(
,0),C(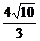 ,试求椭圆的方程
,试求椭圆的方程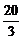 ,椭圆C2的方程为
,椭圆C2的方程为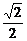 ,如果C1与C2相交于A、B两点,且线段AB恰为圆C1的直径,求直线AB的方程和椭圆C2的方程
,如果C1与C2相交于A、B两点,且线段AB恰为圆C1的直径,求直线AB的方程和椭圆C2的方程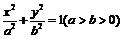 的左、右焦点分别为F1、F2,线段F1F2被抛物线y2=2px的焦点分成5:3两段,则此椭圆的离心率为
( )
的左、右焦点分别为F1、F2,线段F1F2被抛物线y2=2px的焦点分成5:3两段,则此椭圆的离心率为
( ) 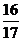 B.
B.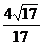 C.
C.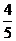 D.
D.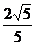
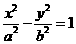 由椭圆
由椭圆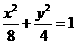 求得两焦点为
求得两焦点为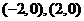 ,
, 对于双曲线
对于双曲线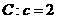 ,又
,又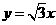 为双曲线
为双曲线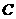 的一条渐近线
的一条渐近线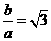 解得
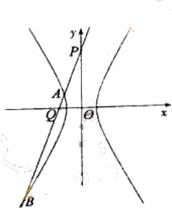
解得 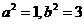 ,
,
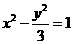
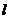 的斜率
的斜率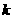 存在且不等于零。
存在且不等于零。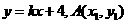 ,
,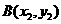 则
则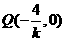
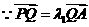
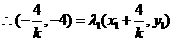
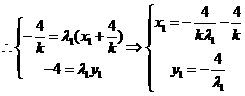

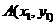 在双曲线
在双曲线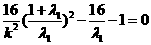
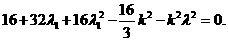
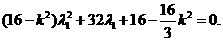
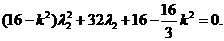
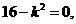 则直线
则直线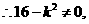
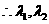 是二次方程
是二次方程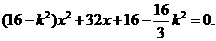 的两根.
的两根.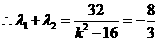
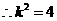 ,
,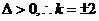 .
.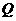 的坐标为
的坐标为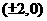 .
.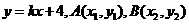 ,则
,则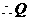 分
分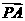 的比为
的比为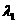 .
.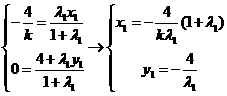
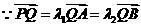 ,
,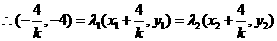 .
.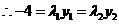 ,
,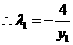 ,
,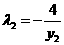 ,
,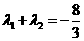 ,
,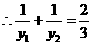 ,即
,即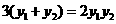
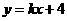 代入
代入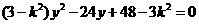
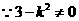 ,否则
,否则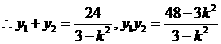 。
。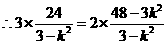
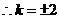
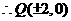
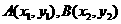 ,则
,则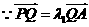 ,
,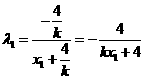
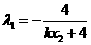
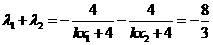 .
.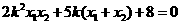 。 (*)
。 (*)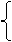 又
又 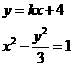
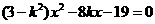 .
.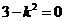 时,则直线l与双曲线得渐近线平行,不合题意,
时,则直线l与双曲线得渐近线平行,不合题意,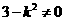 。
。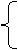
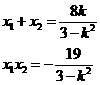
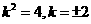
 时,x=
时,x=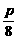 .
.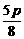 .
.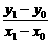 =
=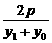 (x1≠x0).
(x1≠x0).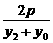 (x2≠x0).
(x2≠x0).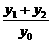 =-2.
=-2.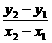 =
=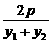 (x1≠x2).
(x1≠x2).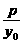 ,所以kAB是非零常数.
,所以kAB是非零常数.