摘要:解 建立坐标系如图所示. 设|AB|=2a,则A(-a,0),B(a,0) 设M(x,y)是轨迹上任意一点 则由题设.得=λ,坐标代入.得=λ,化简得 (1-λ2)x2+(1-λ2)y2+2a(1+λ2)x+(1-λ2)a2=0 (1)当λ=1时.即|MA|=|MB|时.点M的轨迹方程是x=0.点M的轨迹是直线(y轴) (2)当λ≠1时.点M的轨迹方程是x2+y2+x+a2=0 点M的轨迹是以(-.0)为圆心.为半径的圆
网址:http://m.1010jiajiao.com/timu3_id_527149[举报]
如图,为了研究钟表与三角函数的关系,建立了如图所示的坐标系,设秒针针尖位置P(x,y).若初始位置为P0( ,
, ),当秒针从P0(注:此时t=0)正常开始走时,点P的纵坐标y与时间t的函数关系为( )
),当秒针从P0(注:此时t=0)正常开始走时,点P的纵坐标y与时间t的函数关系为( )

 ,
, ),当秒针从P0(注:此时t=0)正常开始走时,点P的纵坐标y与时间t的函数关系为( )
),当秒针从P0(注:此时t=0)正常开始走时,点P的纵坐标y与时间t的函数关系为( )
A.y=sin( t+ t+ ) ) | B.y=sin(- t- t- ) ) |
C.y=sin(- t+ t+ ) ) | D.y=sin(- t- t- ) ) |
如图,为了研究钟表与三角函数的关系,建立了如图所示的坐标系,设秒针针尖位置P(x,y).若初始位置为P0( ,
, ),当秒针从P0(注:此时t=0)正常开始走时,点P的纵坐标y与时间t的函数关系为( )
),当秒针从P0(注:此时t=0)正常开始走时,点P的纵坐标y与时间t的函数关系为( )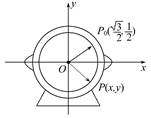
A.y=sin(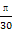 t+ t+ ) ) | B.y=sin(-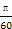 t- t- ) ) |
C.y=sin(-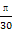 t+ t+ ) ) | D.y=sin(-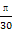 t- t- ) ) |
已知正三棱锥P-ABC的底面边长为6,侧棱长为
.有一动点M在侧面PAB内,它到顶点P的距离与到底面ABC的距离比为2
:1.
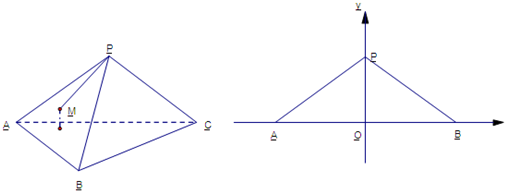
(1)求动点M到顶点P 的距离与它到边AB的距离之比;
(2)在侧面PAB所在平面内建立为如图所示的直角坐标系,求动点M的轨迹方程. 查看习题详情和答案>>
| 13 |
| 2 |

(1)求动点M到顶点P 的距离与它到边AB的距离之比;
(2)在侧面PAB所在平面内建立为如图所示的直角坐标系,求动点M的轨迹方程. 查看习题详情和答案>>
 已知长方体ABCD-A1B1C1D1中,DA=DD1=1,
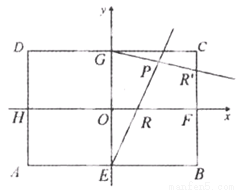
已知长方体ABCD-A1B1C1D1中,DA=DD1=1,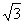 ,|AD|=2,E、F、G、H分别为矩形四条边的中点,以HF、GE所在直线分别为x,y轴建立直角坐标系(如图所示).若R、R′分别在线段0F、CF上,且
,|AD|=2,E、F、G、H分别为矩形四条边的中点,以HF、GE所在直线分别为x,y轴建立直角坐标系(如图所示).若R、R′分别在线段0F、CF上,且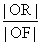 =
=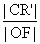 =
=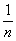 .
.
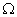 :
: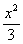 +
+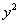 =1上;
=1上;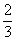 ,求证:直线MN过定点
,求证:直线MN过定点