摘要:解 (1)设P点的坐标为(x1,y1).则Q点坐标为(x1,-y1),又有A1(-m,0),A2(m,0),则A1P的方程为 y= ① A2Q的方程为 y=- ② ①×②得 y2=- ③ 又因点P在双曲线上.故 代入③并整理得=1 此即为M的轨迹方程 (2)当m≠n时.M的轨迹方程是椭圆 (ⅰ)当m>n时.焦点坐标为(±,0).准线方程为x=±,离心率e=, (ⅱ)当m<n时.焦点坐标为(0,±),准线方程为y=±,离心率e=
网址:http://m.1010jiajiao.com/timu3_id_527150[举报]
 已知椭圆
已知椭圆| x2 |
| 3 |
| y2 |
| 2 |
(Ⅰ)设P点的坐标为(x0,y0),证明:
| x02 |
| 3 |
| y02 |
| 2 |
(Ⅱ)求四边形ABCD的面积的最小值. 查看习题详情和答案>>
(本小题满分12分)
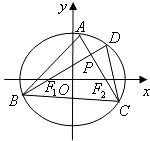
已知椭圆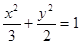 的左、右焦点分别为F1、F2.过F1的直线交椭圆于B、D两点,过F2的直线交椭圆于A、C两点,且AC⊥BD,垂足为P.
的左、右焦点分别为F1、F2.过F1的直线交椭圆于B、D两点,过F2的直线交椭圆于A、C两点,且AC⊥BD,垂足为P.
(Ⅰ)设P点的坐标为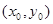 ,证明:
,证明: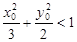 ;
;
(Ⅱ)求四边形ABCD的面积的最小值.
查看习题详情和答案>>
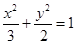 的左、右焦点分别为
的左、右焦点分别为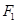 ,
,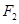 ,过
,过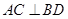 ,垂足为P.
,垂足为P.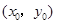 ,证明:
,证明: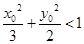 ;
; 已知椭圆
已知椭圆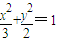 的左右焦点分别为F1、F2,过F1的直线交椭圆于B、D两点,过F2的直线交椭圆于A、C两点,且AC⊥BD,垂足为P
的左右焦点分别为F1、F2,过F1的直线交椭圆于B、D两点,过F2的直线交椭圆于A、C两点,且AC⊥BD,垂足为P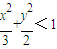 ;
;