摘要：解:(1)当y=时.x=. 又抛物线y2=2px的准线方程为x=-. 由抛物线定义得 所求距离为-(-)=. (2)设直线PA的斜率为kPA.直线PB的斜率为kPB. 由y12=2px1.y02=2px0. 相减得(y1-y0)(y1+y0)=2p(x1-x0). 故kPA==(x1≠x0). 同理可得kPB=(x2≠x0). 由PA.PB倾斜角互补知kPA=-kPB. 即=-.所以y1+y2=-2y0. 故=-2. 设直线AB的斜率为kAB. 由y22=2px2.y12=2px1. 相减得(y2-y1)(y2+y1)=2p(x2-x1). 所以kAB==(x1≠x2). 将y1+y2=-2y0(y0＞0)代入得 kAB==-.所以kAB是非零常数.
网址：http://m.1010jiajiao.com/timu3_id_527141[举报]
已知数列{an}满足，an+1=
．
（1）若方程f（x）=x的解称为函数y=f（x）的不动点，求an+1=f（an）的不动点的值；
（2）若a1=2，bn=
，求证：数列{lnbn}是等比数列，并求数列{bn}的通项．
（3）当任意n∈N*时，求证：b1+b2+b3+…+bn＜
．
查看习题详情和答案>>
an(
| ||
3
|
（1）若方程f（x）=x的解称为函数y=f（x）的不动点，求an+1=f（an）的不动点的值；
（2）若a1=2，bn=
| an-1 |
| an+1 |
（3）当任意n∈N*时，求证：b1+b2+b3+…+bn＜
| 1 |
| 2 |
已知数列{an}满足an+1=
．
（1）若方程f（x）=x的解称为函数y=f（x）的不动点，求an+1=f（an）的不动点的值；
（2）若a1=2，bn=
，求数列{bn}的通项．
（3）当n≥3时，求证：b1+b2+b3+…+bn＜
．
查看习题详情和答案>>
an(
| ||
3
|
（1）若方程f（x）=x的解称为函数y=f（x）的不动点，求an+1=f（an）的不动点的值；
（2）若a1=2，bn=
| an-1 |
| an+1 |
（3）当n≥3时，求证：b1+b2+b3+…+bn＜
| 241 |
| 648 |
已知数列{an}满足，
．
（1）若方程f（x）=x的解称为函数y=f（x）的不动点，求an+1=f（an）的不动点的值；
（2）若a1=2，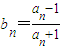
，求证：数列{lnbn}是等比数列，并求数列{bn}的通项．
（3）当任意n∈N*时，求证：b1+b2+b3+…+bn＜
．
查看习题详情和答案>>
．（1）若方程f（x）=x的解称为函数y=f（x）的不动点，求an+1=f（an）的不动点的值；
（2）若a1=2，
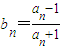，求证：数列{lnbn}是等比数列，并求数列{bn}的通项．（3）当任意n∈N*时，求证：b1+b2+b3+…+bn＜
．查看习题详情和答案>>
．
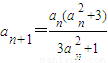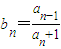，求数列{bn}的通项．
．
，
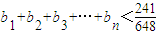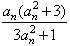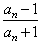，求证：数列{lnbn}是等比数列，并求数列{bn}的通项；
。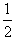