0 52616 52624 52630 52634 52640 52642 52646 52652 52654 52660 52666 52670 52672 52676 52682 52684 52690 52694 52696 52700 52702 52706 52708 52710 52711 52712 52714 52715 52716 52718 52720 52724 52726 52730 52732 52736 52742 52744 52750 52754 52756 52760 52766 52772 52774 52780 52784 52786 52792 52796 52802 52810 447348
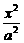 +
+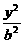 =1,其中a>b>0待定
=1,其中a>b>0待定
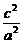 =
=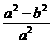 =1-(
=1-(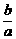 )2
)2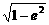 =
=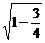 =
=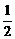 ,即a=2b
,即a=2b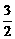 )2=a2(1-
)2=a2(1-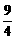
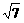 )2=(b+
)2=(b+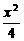 +y2=1
+y2=1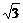 ,-
,-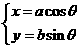 其中a>b>0待定,0≤θ<2π,
其中a>b>0待定,0≤θ<2π,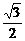 ,∴a=2b
,∴a=2b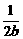 )2+4b2+3
)2+4b2+3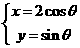
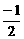 ,cosθ=±
,cosθ=±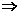 k∈(-1,1),方程所表示的曲线是焦点在x轴上的椭圆; 1-k>3-k2>0
k∈(-1,1),方程所表示的曲线是焦点在x轴上的椭圆; 1-k>3-k2>0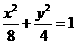 有相同的焦点,直线y=
有相同的焦点,直线y=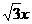 为C的一条渐近线.
为C的一条渐近线.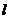 ,交双曲线C于A,B两点,交x轴于Q点(Q点与C的顶点不重合).当
,交双曲线C于A,B两点,交x轴于Q点(Q点与C的顶点不重合).当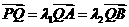 ,且
,且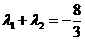 时,求Q点的坐标.
时,求Q点的坐标.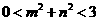
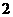 个 5、
个 5、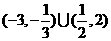
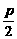 的点到其焦点F的距离;
的点到其焦点F的距离;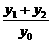 的值,并证明直线AB的斜率是非零常数.
的值,并证明直线AB的斜率是非零常数.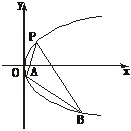
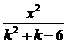 +
+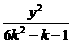 =1表示双曲线的充要条件:__________________.
=1表示双曲线的充要条件:__________________.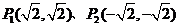 ,
,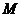 是双曲线
是双曲线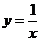 上位于第一象限的点,对于命题①
上位于第一象限的点,对于命题①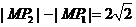 ;②以线段
;②以线段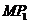 为直径的圆与圆
为直径的圆与圆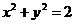 相切;③存在常数
相切;③存在常数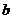 ,使得
,使得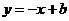 的距离等于
的距离等于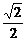
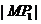 .其中所有正确命题的序号是________.
.其中所有正确命题的序号是________.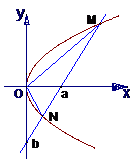 例1.如图,O为坐标原点,直线l在x轴和y轴上的截距分别是a和b(a>0,b≠0),且交抛物线y2=2px(p>0)于M(x1,y1),N(x2,y2)两点
例1.如图,O为坐标原点,直线l在x轴和y轴上的截距分别是a和b(a>0,b≠0),且交抛物线y2=2px(p>0)于M(x1,y1),N(x2,y2)两点
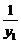 +
+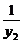 =
=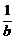 ;(3)当a=2p时,求∠MON的大小
;(3)当a=2p时,求∠MON的大小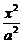 +
+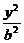 =1(a>b>0),双曲线
=1(a>b>0),双曲线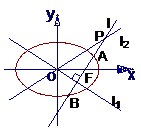 (1)当l1与l2夹角为60°,双曲线的焦距为4时,求椭圆C的方程;
(1)当l1与l2夹角为60°,双曲线的焦距为4时,求椭圆C的方程;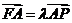 时,求
时,求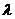 的最大值
的最大值
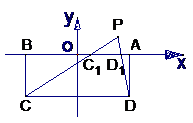
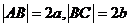 , 以AB边所在的直线为x轴, AB的中点为原点建立直角坐标系, P是x轴上方一点, 使PC、PD与线段AB分别交于
, 以AB边所在的直线为x轴, AB的中点为原点建立直角坐标系, P是x轴上方一点, 使PC、PD与线段AB分别交于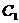 、
、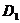 两点, 且
两点, 且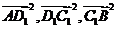 成等比数列, 求动点P的轨迹方程
成等比数列, 求动点P的轨迹方程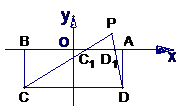
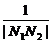 +
+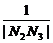 +…+
+…+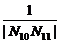 的值.
的值.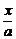 +
+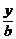 =1
=1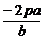 ,y1y2=-2pa
,y1y2=-2pa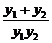 =
=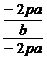 =
=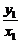 ,k2=
,k2=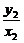
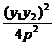 =
=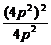 =4p2,
=4p2,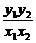 =
=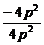 =-1
=-1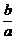 x,两渐近线夹角为60°,
x,两渐近线夹角为60°,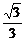
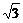 b
b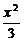 +y2=1
+y2=1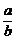 (x-c),与y=
(x-c),与y=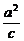 ,
,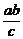 ),
),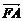 =λ
=λ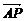 得A(
得A(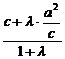 ,
,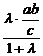 )
)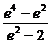 =-[(2-e2)+
=-[(2-e2)+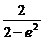 ]+3≤3-2
]+3≤3-2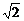
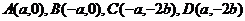 ,
, 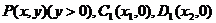 ,
,
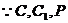 三点共线,
三点共线, 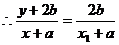 ,
, 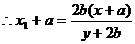 , 又
, 又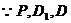 三点共线,
三点共线, 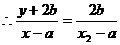 ,
, 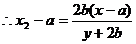 ,
, 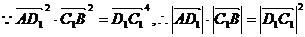 ,
,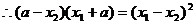 ,
, 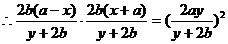 ,
,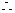 化简得动点P的轨迹方程为
化简得动点P的轨迹方程为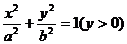
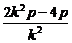 ,y1+y2=k(x1+x2+2p)=
,y1+y2=k(x1+x2+2p)=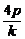 ,
,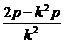 ,
,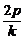 ).
).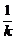 (x-
(x-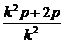 =p+
=p+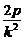 .
.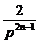 ,0).
,0).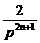 )|=
)|=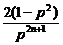 ,
,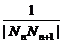 =
=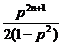 ,
,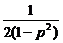 [p3+p4+…+p21]=
[p3+p4+…+p21]=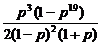 .
.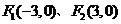 是椭圆
是椭圆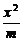 +
+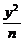 =1的两个焦点,
=1的两个焦点,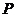 是椭圆上的点,当
是椭圆上的点,当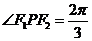 时,
时,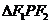 的面积最大,则有
( )
的面积最大,则有
( )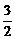 D.m=12,n=6
D.m=12,n=6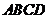 的相对顶点
的相对顶点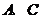 为焦点的椭圆,恰好过正方形四边的中点,则该椭圆的离心率为
( )
为焦点的椭圆,恰好过正方形四边的中点,则该椭圆的离心率为
( )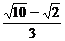 B.
B.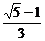 C.
C.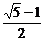 D.
D.