0 52192 52200 52206 52210 52216 52218 52222 52228 52230 52236 52242 52246 52248 52252 52258 52260 52266 52270 52272 52276 52278 52282 52284 52286 52287 52288 52290 52291 52292 52294 52296 52300 52302 52306 52308 52312 52318 52320 52326 52330 52332 52336 52342 52348 52350 52356 52360 52362 52368 52372 52378 52386 447348
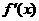 是函数
是函数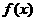 的导函数,将
的导函数,将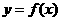 和
和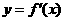 的图象画在同一个直角坐标系中,不可能正确的是(
)
的图象画在同一个直角坐标系中,不可能正确的是(
)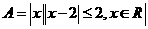 ,
,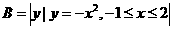 ,则
,则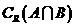 等于(
)
等于(
)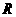 B.
B.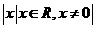 C.
C.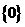 D.
D.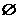
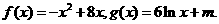
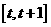 上的最大值
上的最大值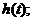
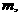 使得
使得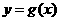 的图象有且只有三个不同的交点?若存在,求出
的图象有且只有三个不同的交点?若存在,求出 的取值范围;若不存在,说明理由。
的取值范围;若不存在,说明理由。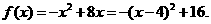
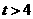 时,(如图11)
时,(如图11)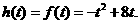
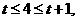 即
即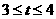 时,
时,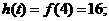
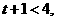 即
即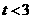 时,
时,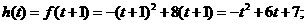
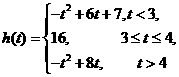
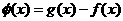 的图象与
的图象与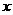 轴的正半轴有且只有三个不同的交点。
轴的正半轴有且只有三个不同的交点。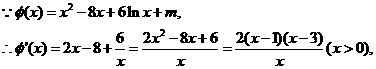
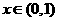 时,
时,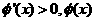 是增函数;
是增函数;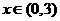 时,
时, 是减函数;
是减函数;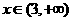 时,
时,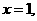 或
或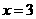 时,
时,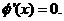
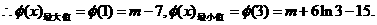
 当
当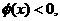 当
当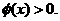
 要使
要使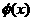 的图象与
的图象与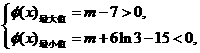 即
即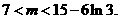
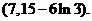
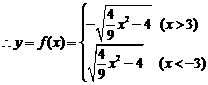
 的值域。
的值域。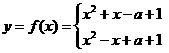
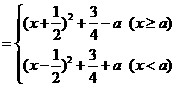
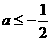 时,如图8知
时,如图8知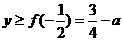
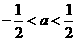 时,如图9
时,如图9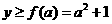
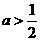 时,如图10
时,如图10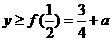
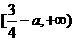
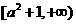
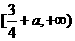
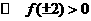
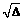 的范围,再转化为a、b的关系,有一定的难度。但是利用数形结合,由二次函数的图象讨论实根分布问题,就容易多了,其压轴功能就大打了折扣。
的范围,再转化为a、b的关系,有一定的难度。但是利用数形结合,由二次函数的图象讨论实根分布问题,就容易多了,其压轴功能就大打了折扣。 -9y
-9y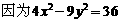 ,故
,故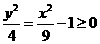
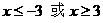 ,
,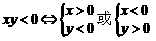
 中,有一个以
中,有一个以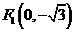 和
和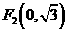 为焦点、离心率为
为焦点、离心率为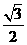 的椭圆,设椭圆在第一象限的部分为曲线C,动点P在C上,C在点P处的切线与
的椭圆,设椭圆在第一象限的部分为曲线C,动点P在C上,C在点P处的切线与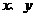 轴的交点分别为A、B,且向量
轴的交点分别为A、B,且向量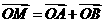 。求:
。求: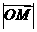 的最小值]。
的最小值]。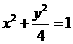 (x>0,y>0)
(x>0,y>0) 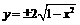 )
)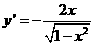 又
又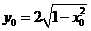 ,
,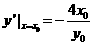 ,
,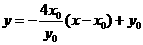
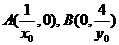 ,又
,又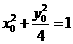 ,设M(x,y)
,设M(x,y)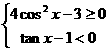
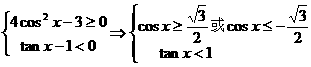
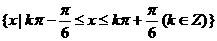
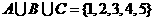 ,且
,且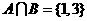 ,求有序集合组{A,B,C}的个数(不同的顺序算不同的组)。
,求有序集合组{A,B,C}的个数(不同的顺序算不同的组)。 C; (2)1∈C且3
C; (2)1∈C且3