0 52106 52114 52120 52124 52130 52132 52136 52142 52144 52150 52156 52160 52162 52166 52172 52174 52180 52184 52186 52190 52192 52196 52198 52200 52201 52202 52204 52205 52206 52208 52210 52214 52216 52220 52222 52226 52232 52234 52240 52244 52246 52250 52256 52262 52264 52270 52274 52276 52282 52286 52292 52300 447348
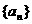 中,
中,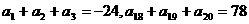 ,则此数列前20项和等于
,则此数列前20项和等于 的图象,可以把函数
的图象,可以把函数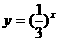 的图象( )
的图象( )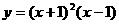 在
在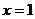 处的导数等于( )
处的导数等于( )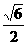 B.
B. 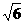 C.
C.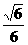 D.
D. 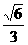
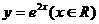 的反函数为( )
的反函数为( )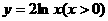 B.
B.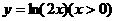
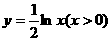 D.
D.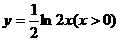
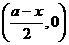 ,A点的坐标为
,A点的坐标为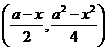 .
.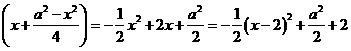 (0<x<a).
(0<x<a).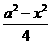 ,两边之比为8:
,两边之比为8: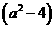 ;
;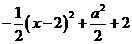 无最大值,也就是说周长最大的内接矩形不存在.
无最大值,也就是说周长最大的内接矩形不存在.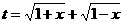 ,要使
,要使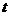 有意义,必须
有意义,必须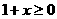 且
且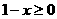 ,即
,即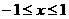 ,
,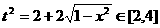 ,且
,且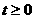 ……①
……① 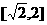 .
.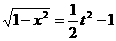 ,
,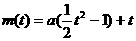
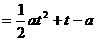 ,
,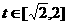 .
.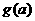 即为函数
即为函数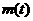
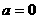 时,
时,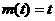 ,
,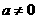 时,此时直线
时,此时直线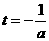 是抛物线
是抛物线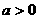 时,函数
时,函数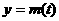 ,
,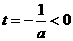 知
知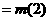
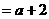 ;
;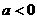 时,,函数
时,,函数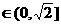 即
即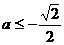 时,
时,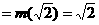 ,
,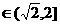 即
即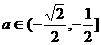 时,
时,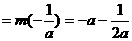 ,
,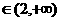 即
即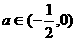 时,
时,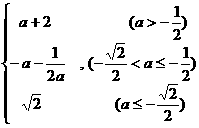 .
.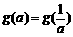 的所有实数a为:
的所有实数a为: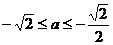 或
或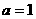 .
.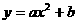 与一次函数图象
与一次函数图象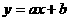 交于两点
交于两点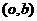 、
、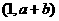 ,由二次函
,由二次函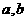 同号,而由
同号,而由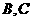 中一次函数图象知
中一次函数图象知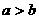 知,当
知,当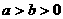 时,
时,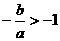 ,此时与
,此时与 中图形不符,当
中图形不符,当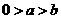 时,
时,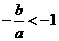 ,与
,与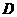 中图形相符.
中图形相符.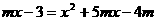 ,
,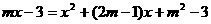 ,
,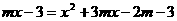 中至少有一个方程有实数解,而此命题的反面是:“三个方程均无实数解”,于是,从全体实数中除去三个方程均无实数解的
中至少有一个方程有实数解,而此命题的反面是:“三个方程均无实数解”,于是,从全体实数中除去三个方程均无实数解的 的值,即得所求.
的值,即得所求.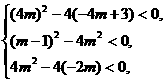 得
得 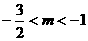 ,
,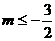 或
或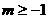 .
.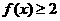 在
在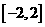 上恒成立,即
上恒成立,即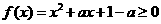 在
在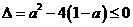 ,
, 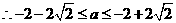 ;
;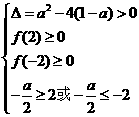 ,
,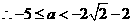 .
.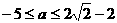 .
.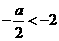 ,即
,即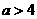 时,应有
时,应有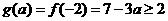 , 即
, 即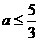 ,
,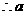 不存在;
不存在;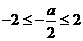 ,即
,即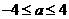 时,应有
时,应有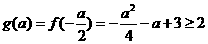 ,
,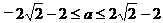 ,
,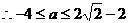 ;
;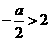 ,即
,即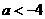 时,应有
时,应有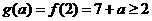 ,即
,即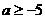 ,
, 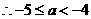
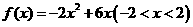 的图象,容易发现在
的图象,容易发现在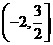 上是增函数,在
上是增函数,在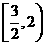 上是减函数,求出
上是减函数,求出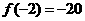 ,
,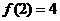 ,
,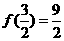 ,注意到函数定义不包含
,注意到函数定义不包含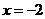 ,所以函数值域是
,所以函数值域是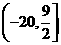 .
.