摘要：向量在空间中的应用.在空间坐标系下.通过向量的坐标的表示.运用计算的方法研究三维空间几何图形的性质. 在复习过程中.抓住源于课本.高于课本的指导方针.本章考题大多数是课本的变式题.即源于课本.因此.掌握双基.精通课本是本章关键.分析近几年来的高考试题.有关平面向量部分突出考查了向量的基本运算.对于和解析几何相关的线段的定比分点和平移等交叉内容.作为学习解析几何的基本工具.在相关内容中会进行考查.本章的另一部分是解斜三角形.它是考查的重点.总而言之.平面向量这一章的学习应立足基础.强化运算.重视应用.考查的重点是基础知识和基本技能.
网址：http://m.1010jiajiao.com/timu3_id_523006[举报]
向量具有鲜明的物理学实际背景,物理学中有两种基本量——标量和矢量,矢量遍布物理学中的很多分支.它包括力、位移、速度等.虽然物理学中的矢量与数学中的向量并不完全相同,如:力除了有大小和方向外还有作用点,而数学中的向量则只有大小和方向,没有作用点.但这并不影响向量在物理学中的应用.请同学们讨论,举出一些物理学中的矢量的例子,并解决下列问题:一位模型赛车手遥控一辆赛车向正东方向前进1 m,逆时针方向转弯α,
继续按直线向前行进1 m.再按逆时针方向转弯α,按直线向前行进1 m.按此方法继续操作下去.如图所示.
(1)作图说明当α=45°时,操作几次时赛车位移为零.
(2)按此方法操作赛车能回到出发点,α应满足什么条件?请写出其中两个.
查看习题详情和答案>>
在平面上，设ha，hb，hc是三角形ABC三条边上的高．P为三角形内任一点，P到相应三边的距离分别为pa，pb，pc，我们可以得到结论：
+
+
=1试通过类比，写出在空间中的类似结论
查看习题详情和答案>>
| pa |
| ha |
| pb |
| hb |
| pc |
| hc |
类比平面上的命题（m），给出在空间中的类似命题（n）的猜想．
（m）如果△ABC的三条边BC，CA，AB上的高分别为ha，hb和hc，△ABC内任意一点P到三条边BC，CA，AB的距离分别为Pa，Pb，Pc，那么
+
+
=1．
（n）
查看习题详情和答案>>
（m）如果△ABC的三条边BC，CA，AB上的高分别为ha，hb和hc，△ABC内任意一点P到三条边BC，CA，AB的距离分别为Pa，Pb，Pc，那么
| pa |
| ha |
| pb |
| hb |
| pc |
| hc |
（n）
设ha，hb，hc，hd为四面体S-ABC的四个面上的高，P为四面体内的任一点，
P到相应四个面的距离分别为Pa，Pb，Pc，pd，那么
+
+
+
=1
P到相应四个面的距离分别为Pa，Pb，Pc，pd，那么
| pa |
| ha |
| pb |
| hb |
| pc |
| hc |
| pd |
| hd |
设ha，hb，hc，hd为四面体S-ABC的四个面上的高，P为四面体内的任一点，
P到相应四个面的距离分别为Pa，Pb，Pc，pd，那么
+
+
+
=1
．P到相应四个面的距离分别为Pa，Pb，Pc，pd，那么
| pa |
| ha |
| pb |
| hb |
| pc |
| hc |
| pd |
| hd |
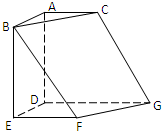如图，在空间中的直角三角形ABC与直角梯形EFGD中，平面ABC∥平面DEFG，AD⊥平面DEFG，AC∥DG．且AB=AD=DE=DG=2，AC=EF=1．
如图，在空间中的直角三角形ABC与直角梯形EFGD中，平面ABC∥平面DEFG，AD⊥平面DEFG，AB∥DE，AC∥DG．且AB=AD=DE=DG=2，AC=EF=1．