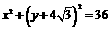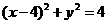0 51663 51671 51677 51681 51687 51689 51693 51699 51701 51707 51713 51717 51719 51723 51729 51731 51737 51741 51743 51747 51749 51753 51755 51757 51758 51759 51761 51762 51763 51765 51767 51771 51773 51777 51779 51783 51789 51791 51797 51801 51803 51807 51813 51819 51821 51827 51831 51833 51839 51843 51849 51857 447348
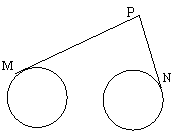 (江苏卷) 如图,圆O1与圆O2的半径都是1,O1O2=4,过动点P分别作圆O1、圆O2的切线PM、PN(M、N分别为切点),使得
(江苏卷) 如图,圆O1与圆O2的半径都是1,O1O2=4,过动点P分别作圆O1、圆O2的切线PM、PN(M、N分别为切点),使得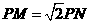 试建立适当的坐标系,并求动点 P的轨迹方程.
试建立适当的坐标系,并求动点 P的轨迹方程.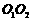 为
为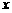 轴,线段
轴,线段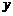 轴,建立平面直角坐标系,则两圆心分别为
轴,建立平面直角坐标系,则两圆心分别为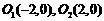 .设
.设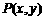 ,则
,则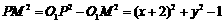 ,同理
,同理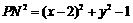 .
.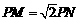 ,
,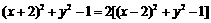 ,
,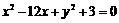 ,即
,即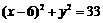 .这就是动点
.这就是动点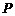 的轨迹方程.
的轨迹方程.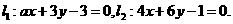 若
若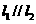 ,则
,则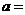 ____.
____.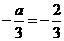 ,则
,则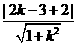 <1,解得kÎ(0,
<1,解得kÎ(0,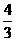 )
)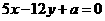 与圆
与圆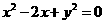 相切,则
相切,则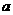 的值为
。
的值为
。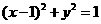 ,所以圆心坐标为(1,0),半径为1,由已知可得
,所以圆心坐标为(1,0),半径为1,由已知可得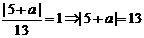 ,所以
,所以 的值为-18或8。
的值为-18或8。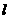 过点
过点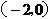 ,当直线
,当直线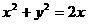 有两个交点时,其斜率k的取值范围是(B)
有两个交点时,其斜率k的取值范围是(B)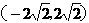 (B)
(B)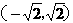
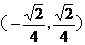 (D)
(D)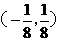
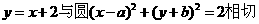 ”的 (A )
”的 (A )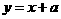 ,圆心(0,0)道直线的距离等于半径
,圆心(0,0)道直线的距离等于半径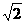 ,∴
,∴ 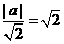 ,∴ a 的值±2,选B.
,∴ a 的值±2,选B. 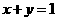 与圆
与圆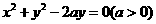 没有公共点,则
没有公共点,则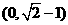 B.
B.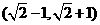 C.
C.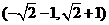 D.
D.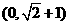
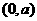 到直线
到直线 ,选A。
,选A。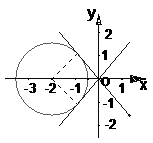 如果实数满足
如果实数满足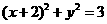 ,求
,求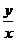 的最大值、2x-y的最小值
的最大值、2x-y的最小值
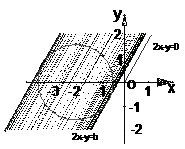 解:(1)问题可转化为求圆
解:(1)问题可转化为求圆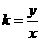 的最大值, 由图形性质可知, 由原点向圆
的最大值, 由图形性质可知, 由原点向圆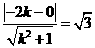 ,解得
,解得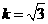 或
或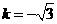
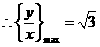
 x,y满足
x,y满足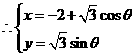
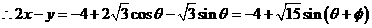
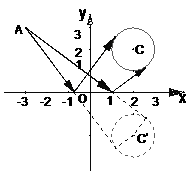 例3.自点A(-3,3)发出的光线
例3.自点A(-3,3)发出的光线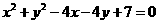 相切,求光线
相切,求光线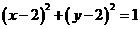 关于x轴对称的圆C‘的方程为
关于x轴对称的圆C‘的方程为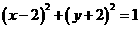 ,其圆心C‘(2,-2),则
,其圆心C‘(2,-2),则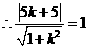 ,
,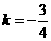 或
或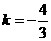 ,
,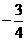 (x+3)或 y-3=
(x+3)或 y-3=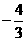 (x+3),
(x+3),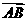 所成的比为
所成的比为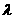 ,证明:
,证明:
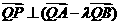 (II)设直线AB的方程是x-2y+12=0,过A,B两点的圆C与抛物线在点A处有共同的切线,求圆C的方程.
(II)设直线AB的方程是x-2y+12=0,过A,B两点的圆C与抛物线在点A处有共同的切线,求圆C的方程.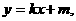 代入抛物线方程
代入抛物线方程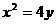 得
得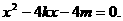 ①
①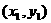 、
、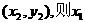 、x2是方程①的两根.
、x2是方程①的两根.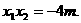
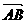 所成的比为
所成的比为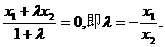
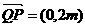 .
.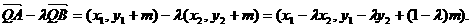
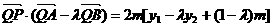
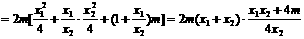
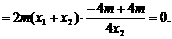
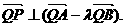
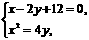 得点A、B的坐标分别是(6,9)、(-4,4).
得点A、B的坐标分别是(6,9)、(-4,4).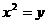 得
得 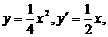 所以抛物线
所以抛物线 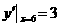
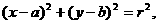 则
则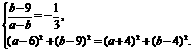
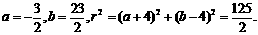
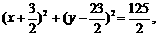 即
即 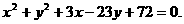
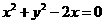 外切,并与直线
外切,并与直线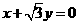 相切于点M(
相切于点M(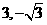 ),求该圆的方程
),求该圆的方程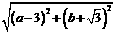 ,
, 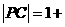
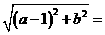 1+
1+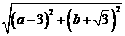 (1)
(1)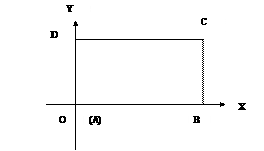 又所求圆与直线
又所求圆与直线 直线
直线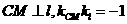 ,于是
,于是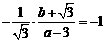 ,
,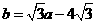 (2) 将(2)代入(1)化简,得a2-4a=0,
(2) 将(2)代入(1)化简,得a2-4a=0, 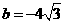 ,所求圆方程为
,所求圆方程为