摘要:(Ⅰ)求B的大小; (Ⅱ)求的取值范围. 某商场经销某商品,根据以往资料统计,顾客采用的付款期为ζ的分布列为 ζ 1 2 3 4 5 P 0.4 0.2 0.2 0.1 0.1 商场经销一件该商品.采用1期付款.基利润为200元,分2期或3期付款.基利润为250元,分4期或5期付款.其利润为300元.η表示经销一件该商品的利润. (Ⅰ)求事件A:“购买该商品的3位顾客中.至少有1件位采用1期付款的概率P(A), (Ⅱ)求η的分布列及期Eη. 四棱锥S-ABCD中.底面ABCD为平行四边形.侧面SBC⊥底面ABCD.已知∠ABC=45°.AB=2.BC=2.SA=SB=. (Ⅰ)证明:SA⊥BC, (Ⅱ)求直线SD与平面SAB所成角的大小. 设函数f(x)=ex-e- x. (Ⅰ)证明:f(x)的导数f'(x)≥2, (Ⅱ)若对所有x=0都有f(x)≥ax.求a的取值范围. 已知椭圆的左.右焦点分别为F1.F2.过F1的直线交椭圆于B.D两点.过F2的直线交椭圆于A.C两点.且AC⊥BD.垂足为P. (Ⅰ)设P点的坐标为(x0.y0).证明:, (Ⅱ)求四过形ABCD的面积的最小值. 已知数列{an}中a1=2.an+1=()(an+2).n=1.2.3-. (Ⅰ)求{an}的通项公式, (Ⅱ)若数列{bn}中b1=2.bn+1=,n=1.2.3.-.证明: -.
网址:http://m.1010jiajiao.com/timu3_id_510931[举报]
 ,且满足
,且满足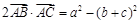 .
.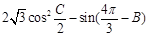 的最大值,并求取得最大值时角B、C的大小.
的最大值,并求取得最大值时角B、C的大小. ,且满足
,且满足 .
. 的最大值,并求取得最大值时角B、C的大小.
的最大值,并求取得最大值时角B、C的大小.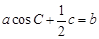 .
.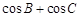 的取值范围。
的取值范围。 .
. 的取值范围。
的取值范围。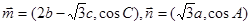 ,
,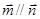 .
.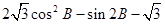 的取值区间。
的取值区间。