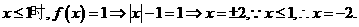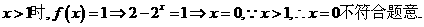22. (本题满分13分)
(理科)已知椭圆的两个焦点分别为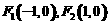 ,过
,过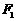 的直线
的直线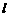 交椭圆于点M、N,
交椭圆于点M、N,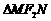 的周长为8.过
的周长为8.过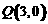 的直线m交椭圆于不同的两点A、B.
的直线m交椭圆于不同的两点A、B.
|
|
(2)OA·OB = 0能否成立(O为原点)?若能成立,求出此时直线m的方程;若不能
|
|
|
|
|
 (3)若在x轴上存在一点C,使AB·(CA+ AB)= 0成立,求|OC|的取值范围.
(3)若在x轴上存在一点C,使AB·(CA+ AB)= 0成立,求|OC|的取值范围.
[解析]
(1)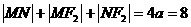 --------2分
--------2分 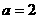 ,
,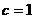 ,
,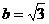 -
-
所以椭圆的方程为: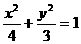 ---------3分
---------3分
(2)若直线 :
: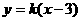 使
使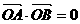 成立,设
成立,设 ,
,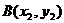
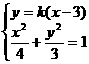 消去
消去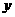 得:
得: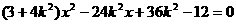
由 ,得
,得 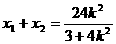 ,
,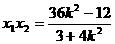
∵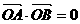 ∴
∴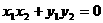
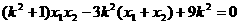 解得
解得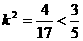
故存在直线 :
: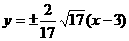 满足条件。-------8分
满足条件。-------8分
-(3)由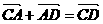 故
故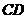 垂直
垂直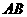
直线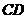 的方程为:
的方程为: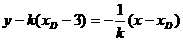
令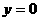 ,得
,得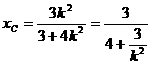
因为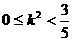 ,所以
,所以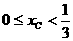 故
故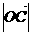 的取值范围为
的取值范围为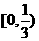 -----13分
-----13分
[评析] 本题综合考查了椭圆的定义、标准方程、直线与椭圆、向量等知识的灵活运用,运用韦达定理设而不求是处理直线与圆锥曲线位置关系,是解析几何中减少运算量一种重要手段。
(文科)平面直角坐标系中,O为坐标原点,给定两点A(1,0)、B(0,-2),点C满足
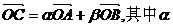 、
、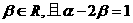
(1)求点C的轨迹方程;
(2)设点C的轨迹与双曲线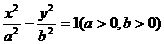 交于两点M、N,且以MN为直径的圆过原点,求证:
交于两点M、N,且以MN为直径的圆过原点,求证: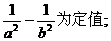
(3)在(2)的条件下,若双曲线的离心率不大于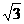 ,求双曲线实轴长的取值范围.
,求双曲线实轴长的取值范围.
(1)解:设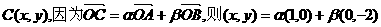
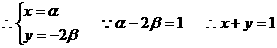
即点C的轨迹方程为x+y=1……(4分)
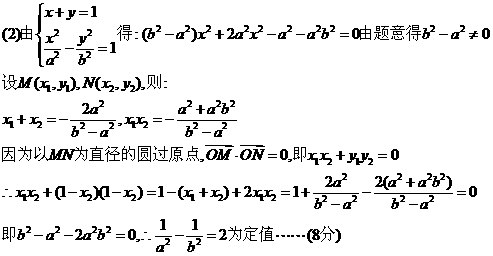
(3)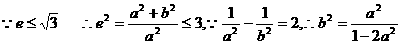
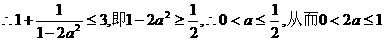
∴双曲线实轴长的取值范围是(0,1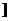 ………………(13分)
………………(13分)
[评析] 本题综合考查了向量与点的轨迹、直线与圆锥曲线的位置关系的灵活运用、椭圆的几何性质等,要注意综合分析后,采用适当的方法减少运算量.
[命题报告]
命题前对近几年来高考的热点、难点和重点进行了全面的研究,命题时依据最新的《考试大纲》的各项要求,.融入了新课程新大纲的理念,在注重对基础知识的全面考查的同时,注重对考生创造性地解决问题能力的考查。
21.(本题满分13分)
(理科)已知 ,数列{an}满足:
,数列{an}满足: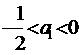 ,
,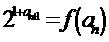 ,
,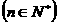 .
.
(1)
求证: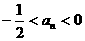
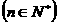 .
.
(2)
判断an与an+1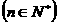 的大小,并说明理由。
的大小,并说明理由。
[解析]
|
|

由①,②可知,
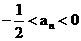 对于任意
对于任意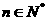 都成立.
都成立.
|
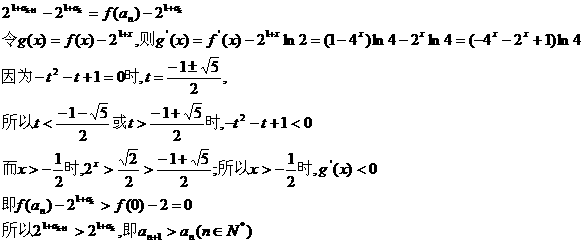 [评析] 本题在函数、数列、不等式等知识交汇处命题,综合考查考生分析解决问题的能力。在数学归纳法中运用求导是本题的新亮点,探询传统知识和新增知识的整合在本题得到较完美的体现。
[评析] 本题在函数、数列、不等式等知识交汇处命题,综合考查考生分析解决问题的能力。在数学归纳法中运用求导是本题的新亮点,探询传统知识和新增知识的整合在本题得到较完美的体现。
(文科)定义:若数列 对任意
对任意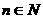 ,满足
,满足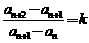 (k为常数),则称数列
(k为常数),则称数列 为等差比数列.
为等差比数列.
(1)若数列 的前n 项和
的前n 项和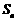 满足
满足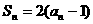 ,求
,求 的通项公式,并判断数列
的通项公式,并判断数列
是否为等差比数列;
(2)若数列 为等差数列,试判断
为等差数列,试判断 是否一定为等差比数列,并说明理由;
是否一定为等差比数列,并说明理由;
(3)试写出一个等差比数列的通项公式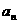 ,使此数列既不是等差数列,也不是等比数列.
,使此数列既不是等差数列,也不是等比数列.
[解析]
(1)当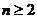 时,
时,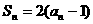 ①,
①,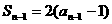 ②-
②-
①-②得: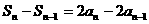 所以
所以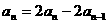
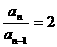
又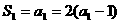 ,所以
,所以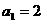 ,所以
,所以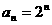 (
(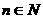 )
)
∵任给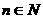 ,
,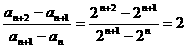 ∴数列
∴数列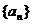 为等差比数列…..5分
为等差比数列…..5分
(2)令等差数列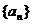 的公差为
的公差为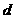 ,则
,则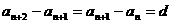
当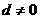 时,
时,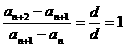 (1为常数),所以数列
(1为常数),所以数列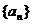 是等差比数列-
是等差比数列-
当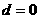 ,即数列
,即数列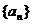 是常数数列时,不是等差比数列。。。。。。。。10分
是常数数列时,不是等差比数列。。。。。。。。10分
(3)通项如 形式的数列,如
形式的数列,如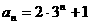 ,不是等差数列,也不是等比数列,但
,不是等差数列,也不是等比数列,但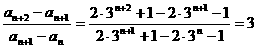 为常数。
为常数。
数列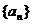 是等差比数列--------------13分(只要写出一个通项即可)
是等差比数列--------------13分(只要写出一个通项即可)
[评析] 本题设计新颖,既考查了数列中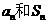 的关系问题等数列的基础知识,又考查了考生理解和学习新知识的能力。
的关系问题等数列的基础知识,又考查了考生理解和学习新知识的能力。
18. (本题满分12分)
设函数
(1)求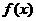 的单调区间和极值;
的单调区间和极值;
(2)讨论方程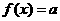 的实根的个数.
的实根的个数.
[解析](1)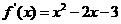 ;由
;由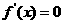 ,得x=-1或x=3.............2分
,得x=-1或x=3.............2分
列表如下:
|
x |
(-∞,-1) |
-1 |
(-1, 3) |
3 |
(3,+ ∞) |
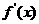 |
- |
0 |
+ |
0 |
- |
|
f(x) |
 |
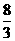 |
 |
-8 |
 |
∴函数f(x)的极大值为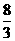 ,极小值为-8
,极小值为-8
函数f(x)单调递增区间是(-∞,-1)和(3,+ ∞),递减区间是(-1, 3)……(6分)
(2)令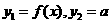 ,根据(1)的分析,可在同一坐标系内作出它们的大致图象,其中
,根据(1)的分析,可在同一坐标系内作出它们的大致图象,其中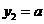 是一条与x轴平行的可移动的平行直线.
是一条与x轴平行的可移动的平行直线.
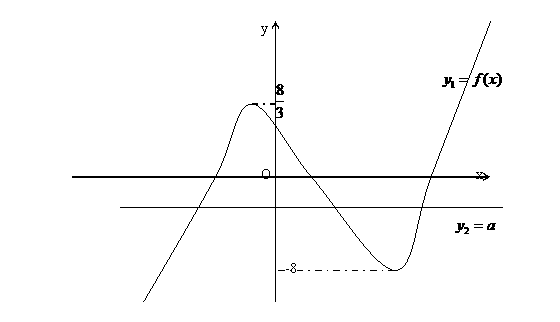

…………………………………………………………………………….9分
∴①当a=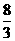 或a=-8时,原方程有且仅有两个不相等的实数根;……10分
或a=-8时,原方程有且仅有两个不相等的实数根;……10分
②当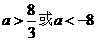 时,原方程有且仅有一个实数根;……………………11分
时,原方程有且仅有一个实数根;……………………11分
③当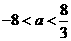 时,原方程有三个实数根……………………………………12分
时,原方程有三个实数根……………………………………12分
[评析]本题考查了导数的运用及三次方程实数根的情况,为利用导数知识来分析三次方程的实根个数提供了新的研究视角。第一问属于基础知识,第二问,借助数形结合的方法,把方程根的个数问题转化为图象交点个数问题,并利用导数知识,分析三次函数的性质,从而作出三次函数的大致图象,为数形结合解决问题提供了保证。
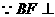 平面ACE.
平面ACE. 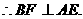
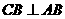 ,
, 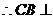 平面ABE.
平面ABE.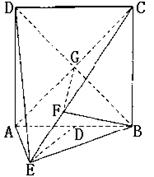
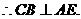
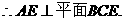
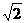 ,
,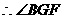 是二面角B-AC-E的平面角.
是二面角B-AC-E的平面角. ,
, 直角
直角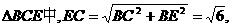
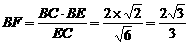 ,
,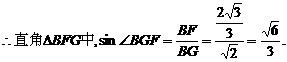
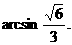
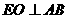 交AB于点O. OE=1.
交AB于点O. OE=1.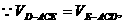
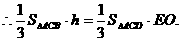
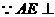 平面BCE,
平面BCE,
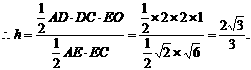
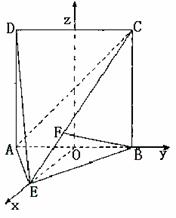 线为x轴,AB所在直线为y轴,过O点平行
线为x轴,AB所在直线为y轴,过O点平行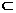 面BCE,
面BCE, 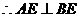 ,
,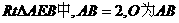 的中点,
的中点,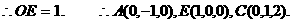
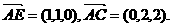 设平面AEC的一个法向量为
设平面AEC的一个法向量为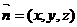 ,
,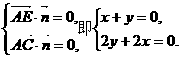
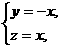
 得
得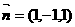 是平面AEC的一个法向量.
是平面AEC的一个法向量.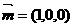 ,
,
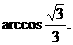
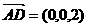 ,
,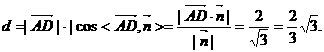
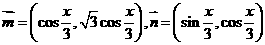 ,
,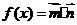
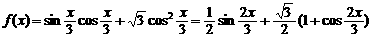 ………………..2分
………………..2分
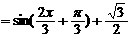 ………………………………………………4分
由
………………………………………………4分
由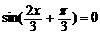 得:
得: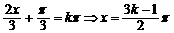 (k∈Z)
∴对称中心的横坐标为
(k∈Z)
∴对称中心的横坐标为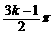 (k∈Z).………………………………………………5分
(k∈Z).………………………………………………5分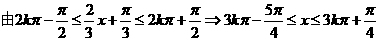
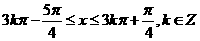 …………………….. 6分
(2)由已知得
…………………….. 6分
(2)由已知得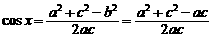 ≥
≥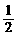 …………………………………8分
又x是△ABC的内角,∴x的取值范围是
…………………………………8分
又x是△ABC的内角,∴x的取值范围是 …………………………………….10分
这时,
…………………………………….10分
这时,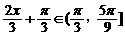 ,∴
,∴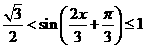 故函数f (x)的值域是
故函数f (x)的值域是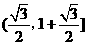 .………………………………………………….12分
.………………………………………………….12分
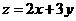 ,由题意可得
,由题意可得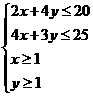
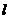 :
: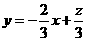 ,当直线
,当直线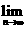 =
=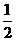
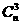 个三元子集,其中含1的三元子集有
个三元子集,其中含1的三元子集有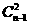 个,
个,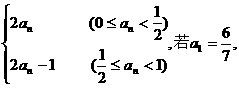 则a20的值是
则a20的值是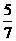
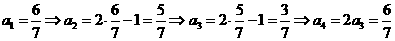 。
。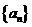 是周期为3的数列,∴
是周期为3的数列,∴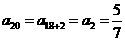 .
.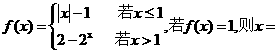 -2
-2