摘要： 本题共有2个小题.第1小题满分6分.第2小题满分8分. 已知正三棱锥的体积为.侧面与底面所成的二面角的大小为.(1)证明:, (2)求底面中心到侧面的距离. [证明](1)取边的中点.连接.. 则..故平面. -- 4分 ∴ . -- 6分 [解]可知平面平面.则是侧面与底面所成二面角的平面角. 过点作为垂足.则就是点到侧面的距离. -- 9分 设为.由题意可知点在上. ∴ .. , -- 11分 ∴ . ∵ .∴ . 即底面中心到侧面的距离为3. -- 14分
网址：http://m.1010jiajiao.com/timu3_id_498733[举报]
本题共有2个小题，第1小题满分6分，第2小题满分10分．
已知a为实数，f(x)=a-
(x∈R)．
（1）求证：对于任意实数a，y=f（x）在（-∞，+∞）上是增函数；
（2）当f（x）是奇函数时，若方程f-1（x）=log2（x+t）总有实数根，求实数t的取值范围．
查看习题详情和答案>>
已知a为实数，f(x)=a-
| 2 | 2x+1 |
（1）求证：对于任意实数a，y=f（x）在（-∞，+∞）上是增函数；
（2）当f（x）是奇函数时，若方程f-1（x）=log2（x+t）总有实数根，求实数t的取值范围．
（2005•上海模拟）本题共有2个小题，第1小题满分8分，第2小题满分6分过直角坐标平面xOy中的抛物线y2?2px （p＞0）的焦点F作一条倾斜角为
| π | 4 |
（1）用p表示A、B之间的距离并写出以AB为直径的圆C方程；
（2）若圆C于y轴交于M、N两点，写出M、N的坐标，证明∠MFN的大小是与p无关的定值，并求出这个值．
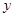（元）与月处理量
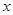（吨）之间的函数关系式可近似的表示为：
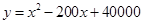，且每处理一吨二氧化碳得到可利用的化工产品价值为300元。
的周长为
，且
．
的值；
（结果用反三角函数值表示）．
两地连线上的定点
处建造广告牌
，其中
为顶端，
长35米，
长80米，设
和
看
.
，问
求