摘要：如图.已知 ..现以A点为位似中心.相似比为9:4.将OB向右侧放大.B点的对应点为C． (1)求C点坐标及直线BC的解析式; (2)一抛物线经过B.C两点.且顶点落在x轴正半轴上.求该抛物线的解析式并画出函数图象; (3)现将直线BC绕B点旋转与抛物线相交与另一点P.请找出抛物线上所有满足到直线AB距离为的点P． 答案:解: (1)过C点向x轴作垂线.垂足为D.由位似图形性质可知: △ABO∽△ACD. ∴． 由已知.可知: ． ∴．∴C点坐标为． 直线BC的解析是为: 化简得: (2)设抛物线解析式为.由题意得: . 解得: ∴解得抛物线解析式为或． 又∵的顶点在x轴负半轴上.不合题意.故舍去． ∴满足条件的抛物线解析式为 (准确画出函数图象) (3) 将直线BC绕B点旋转与抛物线相交与另一点P.设P到 直线AB的距离为h. 故P点应在与直线AB平行.且相距的上下两条平行直线和上． 由平行线的性质可得:两条平行直线与y轴的交点到直线BC的距离也为． 如图.设与y轴交于E点.过E作EF⊥BC于F点. 在Rt△BEF中.. ∴．∴可以求得直线与y轴交点坐标为 同理可求得直线与y轴交点坐标为 ∴两直线解析式,． 根据题意列出方程组: ⑴,⑵ ∴解得:,,, ∴满足条件的点P有四个.它们分别是....
网址：http://m.1010jiajiao.com/timu3_id_480175[举报]
如图，已知 
，
，现以A点为位似中心，相似比为9:4，将OB向右侧放大，B点的对应点为C．
（1）求C点坐标及直线BC的解析式;
（2）一抛物线经过B、C两点，且顶点落在x轴正半轴上，求该抛物线的解析式并画出函数图象;
（3）现将直线BC绕B点旋转与抛物线相交与另一点P，请找出抛物线上所有满足到直线AB距离为
的点P．
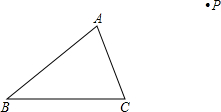如图，已知△ABC．现要将△ABC进行平移，并使点A移动到点P的位置，得到新的△PMN，请画出平移后的△PMN．如图（14），已知 
，
，现以A点为位似中心，相似比为9:4，将OB向右侧放大，B点的对应点为C．
1.求C点坐标及直线BC的解析式;
2.一抛物线经过B、C两点，且顶点落在x轴正半轴上，求该抛物线的解析式并画出函数图象;
3.现将直线BC绕B点旋转与抛物线相交于另一点P，请找出抛物线上所有满足到直线AB距离为
的点P．
查看习题详情和答案>>
，
，现以A点为位似中心，相似比为9:4，将OB向右侧放大，B点的对应点为C．
的点P．
,现需将该纸片剪拼成一个与它面积相等的平行四边形纸片.如果限定裁剪线最多有两条，能否做到： （用“能”或“不能”填空）.若“能”，请确定裁剪线的位置，并说明拼接方法；若填“不能”，请简要说明理由. 