摘要:26.如图所示.在平面直角坐标系中.矩形的边在轴的负半轴上.边在轴的正半轴上.且..矩形绕点按顺时针方向旋转后得到矩形.点的对应点为点.点的对应点为点.点的对应点为点.抛物线过点. (1)判断点是否在轴上.并说明理由, (2)求抛物线的函数表达式, (3)在轴的上方是否存在点.点.使以点为顶点的平行四边形的面积是矩形面积的2倍.且点在抛物线上.若存在.请求出点.点的坐标,若不存在.请说明理由. 解:(1)点在轴上················································· 1分 理由如下: 连接.如图所示.在中... . 由题意可知: 点在轴上.点在轴上.········································································· 3分 (2)过点作轴于点 . 在中.. 点在第一象限. 点的坐标为·························································································· 5分 由(1)知.点在轴的正半轴上 点的坐标为 点的坐标为···························································································· 6分 抛物线经过点. 由题意.将.代入中得 解得 所求抛物线表达式为:······················································· 9分 (3)存在符合条件的点.点.········································································· 10分 理由如下:矩形的面积 以为顶点的平行四边形面积为. 由题意可知为此平行四边形一边. 又 边上的高为2··································································································· 11分 依题意设点的坐标为 点在抛物线上 解得.. . 以为顶点的四边形是平行四边形. .. 当点的坐标为时. 点的坐标分别为., 当点的坐标为时. 点的坐标分别为..··············································· 14分
网址:http://m.1010jiajiao.com/timu3_id_480109[举报]
如图所示,在平面直角坐标系中,点B的坐标为(-3,-4),线段OB绕原点逆时针旋转后 与x轴的正半轴重合,点B的对应点为点A.
与x轴的正半轴重合,点B的对应点为点A.
(1)直接写出点A的坐标,并求出经过A,O,B三点的抛物线的解析式;
(2)在抛物线的对称轴上是否存在点C,使BC+OC的值最小?若存在,求出点C的坐标,若不存在,请说明理由;
(3)如果点P是抛物线上的一个动点,且在x轴的上方,当点P运动到什么位置时,△PAB的面积最大?求出此时点P的坐标和△PAB的最大面积. 查看习题详情和答案>>
 与x轴的正半轴重合,点B的对应点为点A.
与x轴的正半轴重合,点B的对应点为点A.(1)直接写出点A的坐标,并求出经过A,O,B三点的抛物线的解析式;
(2)在抛物线的对称轴上是否存在点C,使BC+OC的值最小?若存在,求出点C的坐标,若不存在,请说明理由;
(3)如果点P是抛物线上的一个动点,且在x轴的上方,当点P运动到什么位置时,△PAB的面积最大?求出此时点P的坐标和△PAB的最大面积. 查看习题详情和答案>>
如图所示,在平面直角坐标系xOy中,正方形OABC的边长为2cm,点A、C分别在y轴的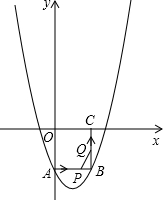 负半轴和x轴的正半轴上,抛物线y=
负半轴和x轴的正半轴上,抛物线y=
x2+bx+c经过点A、B.
(1)求抛物线的表达式.
(2)如果点P由点A开始沿AB边以2cm/s的速度向点B移动,同时点Q由点B开始沿BC以1cm/s的速度向点C移动,当其中一点到达终点时,另一点也随之停止运动.
①移动开始后,是否存在某一时刻t,使得以O、A、P为顶点的三角形与△BPQ相似,若存在,请求出此时t的值,若不存在,请说明理由.
②移动开始后第t秒时,设S=PQ2(cm2),当S取得最小值时,在抛物线上是否存在点R,使得以P、B、Q、R为顶点的四边形是平行四边形?如果存在,求出R点的坐标;如果不存在,请说明理由.
(3)若此抛物线上有一点D(3,
),在抛物线的对称轴上求点M,使得M到D、A的距离之差最大,求出点M的坐标.
查看习题详情和答案>>
 负半轴和x轴的正半轴上,抛物线y=
负半轴和x轴的正半轴上,抛物线y=| 5 |
| 6 |
(1)求抛物线的表达式.
(2)如果点P由点A开始沿AB边以2cm/s的速度向点B移动,同时点Q由点B开始沿BC以1cm/s的速度向点C移动,当其中一点到达终点时,另一点也随之停止运动.
①移动开始后,是否存在某一时刻t,使得以O、A、P为顶点的三角形与△BPQ相似,若存在,请求出此时t的值,若不存在,请说明理由.
②移动开始后第t秒时,设S=PQ2(cm2),当S取得最小值时,在抛物线上是否存在点R,使得以P、B、Q、R为顶点的四边形是平行四边形?如果存在,求出R点的坐标;如果不存在,请说明理由.
(3)若此抛物线上有一点D(3,
| 1 |
| 2 |
如图所示,在平面直角坐标系中,现将直角△ABC放在第二象限,斜靠在两坐标轴上,且∠ACB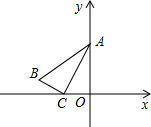 =90°,BC=
=90°,BC=
,点A(0,2),点C(-1,0).抛物线y=ax2+
ax-12a-3经过点B.
(1)求点B的坐标;
(2)求抛物线的解析式;
(3)在抛物线上是否还存在点P(点B除外),使△ACP仍然是以AC为直角边的直角三角形且与△ABC相似?若存在,求所有满足条件的点P的坐标;若不存在,请说明理由. 查看习题详情和答案>>
 =90°,BC=
=90°,BC=
| ||
| 2 |
| 1 |
| 5 |
(1)求点B的坐标;
(2)求抛物线的解析式;
(3)在抛物线上是否还存在点P(点B除外),使△ACP仍然是以AC为直角边的直角三角形且与△ABC相似?若存在,求所有满足条件的点P的坐标;若不存在,请说明理由. 查看习题详情和答案>>
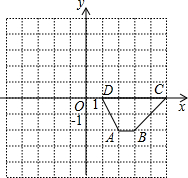 -2),C(5,0),D(1,0),将梯形ABCD绕点D逆时针旋转90°得到梯形A1B1C1D.
-2),C(5,0),D(1,0),将梯形ABCD绕点D逆时针旋转90°得到梯形A1B1C1D.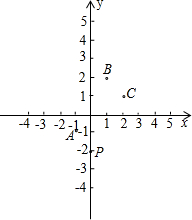 如图所示,在平面直角坐标系中,一颗棋子从点P处开始依次关于点A,B,C作循环对称跳动,即第一次从点P跳到关于点A的对称点M处,第二次从点M跳到关于点B的对称点N处,第三次从点N跳到关于点C的对称点处,…如此下去.
如图所示,在平面直角坐标系中,一颗棋子从点P处开始依次关于点A,B,C作循环对称跳动,即第一次从点P跳到关于点A的对称点M处,第二次从点M跳到关于点B的对称点N处,第三次从点N跳到关于点C的对称点处,…如此下去.