0 47361 47369 47375 47379 47385 47387 47391 47397 47399 47405 47411 47415 47417 47421 47427 47429 47435 47439 47441 47445 47447 47451 47453 47455 47456 47457 47459 47460 47461 47463 47465 47469 47471 47475 47477 47481 47487 47489 47495 47499 47501 47505 47511 47517 47519 47525 47529 47531 47537 47541 47547 47555 447348
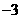 的倒数是…………………………………………………………………………[ ]
的倒数是…………………………………………………………………………[ ]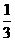 B.
B.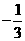 C.
C.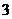 D.
D.
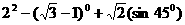

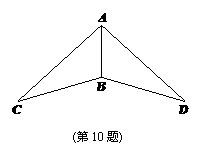 (2)连接AE,AF.若∠ABC=∠ABD,请你证明△ABE≌△ABF.
(2)连接AE,AF.若∠ABC=∠ABD,请你证明△ABE≌△ABF.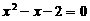 的一个根,则代数式
的一个根,则代数式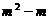 的值等于
.
的值等于
.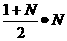
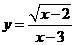 中,自变量
中,自变量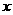 的取值范围是______________
的取值范围是______________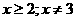
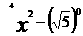

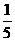 B.
B.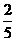 C.
C.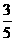 D.1
D.1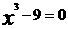 的根最接近(
)
的根最接近(
) 18.(浙江省2008)如图,在平面直角坐标系中,已知点
18.(浙江省2008)如图,在平面直角坐标系中,已知点 坐标为(2,4),直线
坐标为(2,4),直线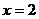 与
与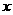 轴相交于点
轴相交于点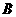 ,连结
,连结 ,抛物线
,抛物线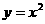 从点
从点 沿
沿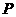 ,顶点
,顶点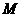 到
到 ,
,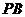 最短;
最短;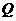 ,使△
,使△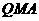
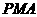 的面积相等,若存在,请求出点
的面积相等,若存在,请求出点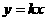 ,
,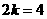 ,
, 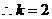 ,
,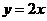 .
.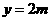 (0≤
(0≤ ).
).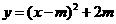 .
.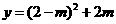
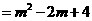 (0≤
(0≤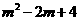 ).
).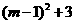 , 又∵0≤
, 又∵0≤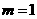 时,PB最短.
时,PB最短.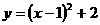 .
.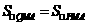 .
.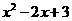 ).
).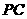 //
// ,交
,交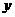 轴于点
轴于点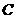 ,
,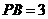 ,
,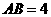 ,
,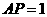 ,∴
,∴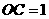 ,∴
,∴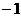 ).
).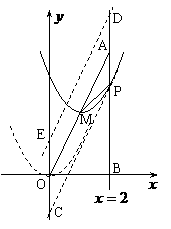 ∵点
∵点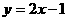 .
.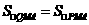 ,∴点
,∴点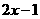 .
.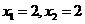 ,即点
,即点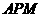 的面积
的面积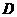 ,过
,过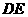 //
//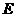 ,
,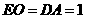 ,∴
,∴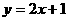 .
.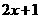 .
.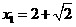 ,
,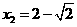 .
.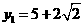 ,
,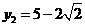 .
.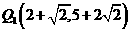 ,
,