摘要:课本中,用具体的函数利用描点法得出正比例函数和一次函数的图象都是一条直线.既然是一条直线.我们只要描出两点即可确定该直线.因为正比例函数是过原点的直线.当然坐标原点是所描的两点中的一个.另外一个是时y=k就是点.所以正比例函数的图像是过两点的直线.而一次函数与两条坐标轴各有一个交点(注意:与x轴.y轴交点的坐标是极其重要的).那么“两点确定一条直线 中的两点就可以取这两个交点.由于一次函数与x轴的交点必在x轴上,而在x轴上的点的特点是纵坐标为0.即:在一次函数中.当y=0时可得kx+b=0.解此方程得x=-.从而得出一次函数与x轴交于(-.0)点,同理.由一次函数与y轴交点的横坐标为0可以得出:它与y轴的交点为(0.b),因此一次函数的图象是过它与x轴的交点(-.0)和它与y轴的交点(0.b)两点的直线.(实践证明.很多同学不会求直线与轴的交点坐标.这是不会解一些一次函数题目的直接原因).例如描述的图象:令,令,所以的图像是过轴上的和x轴上的(.0)两点的直线. x A(0,5)
网址:http://m.1010jiajiao.com/timu3_id_450401[举报]
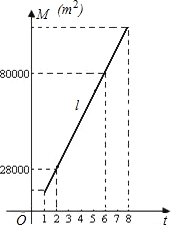 容积率t是指在房地产开发中建筑面积与用地面积之比.为充分利用土地资源,更好地解决人们的住房需求,并适当的控制建筑物的高度,一般地容积率t不小于1且不大于8.一房地产开发商在开发某小区时,结合往年开发经验知,建筑面积M(m2)与容积率t的关系可近似地用如图中的线段l来表示.
容积率t是指在房地产开发中建筑面积与用地面积之比.为充分利用土地资源,更好地解决人们的住房需求,并适当的控制建筑物的高度,一般地容积率t不小于1且不大于8.一房地产开发商在开发某小区时,结合往年开发经验知,建筑面积M(m2)与容积率t的关系可近似地用如图中的线段l来表示.试求图中线段l的函数关系式,并求出开发该小区的用地面积. 查看习题详情和答案>>
容积率t是指在房地产开发中建筑面积与用地面积之比,即t=
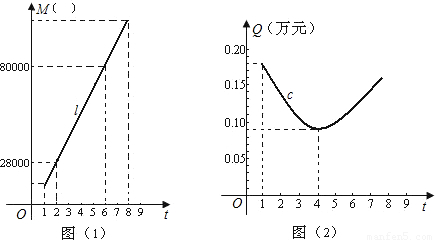
,为充分利用土地资源,更好地解决人们的住房需求,并适当的控制建筑物的高度,一般地容积率t不小于1且不大于8.一房地产开发商在开发某小区时,结合往年开发经验知,建筑面积M(m2)与容积率t的关系可近似地用如图(1)中的线段l来表示;1 m2建筑面积上的资金投入Q(万元)与容积率t的关系可近似地用如图(2)中的一段抛物线段c来表示.
(Ⅰ)试求图(1)中线段l的函数关系式,并求出开发该小区的用地面积;
(Ⅱ)求出图(2)中抛物线段c的函数关系式.
 查看习题详情和答案>>
查看习题详情和答案>>
| M建筑面积 | S用地面积 |
(Ⅰ)试求图(1)中线段l的函数关系式,并求出开发该小区的用地面积;
(Ⅱ)求出图(2)中抛物线段c的函数关系式.
 查看习题详情和答案>>
查看习题详情和答案>>
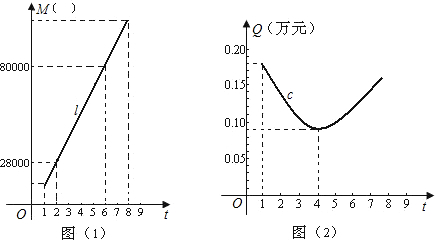
容积率t是指在房地产开发中建筑面积与用地面积之比,即t= ,为充分利用土地资源,更好地解决人们的住房需求,并适当的控制建筑物的高度,一般地容积率t不小于1且不大于8.一房地产开发商在开发某小区时,结合往年开发经验知,建筑面积M(m2)与容积率t的关系可近似地用如图(1)中的线段l来表示;1 m2建筑面积上的资金投入Q(万元)与容积率t的关系可近似地用如图(2)中的一段抛物线段c来表示.
,为充分利用土地资源,更好地解决人们的住房需求,并适当的控制建筑物的高度,一般地容积率t不小于1且不大于8.一房地产开发商在开发某小区时,结合往年开发经验知,建筑面积M(m2)与容积率t的关系可近似地用如图(1)中的线段l来表示;1 m2建筑面积上的资金投入Q(万元)与容积率t的关系可近似地用如图(2)中的一段抛物线段c来表示.
(Ⅰ)试求图(1)中线段l的函数关系式,并求出开发该小区的用地面积;
(Ⅱ)求出图(2)中抛物线段c的函数关系式.

查看习题详情和答案>>
 ,为充分利用土地资源,更好地解决人们的住房需求,并适当的控制建筑物的高度,一般地容积率t不小于1且不大于8.一房地产开发商在开发某小区时,结合往年开发经验知,建筑面积M(m2)与容积率t的关系可近似地用如图(1)中的线段l来表示;1 m2建筑面积上的资金投入Q(万元)与容积率t的关系可近似地用如图(2)中的一段抛物线段c来表示.
,为充分利用土地资源,更好地解决人们的住房需求,并适当的控制建筑物的高度,一般地容积率t不小于1且不大于8.一房地产开发商在开发某小区时,结合往年开发经验知,建筑面积M(m2)与容积率t的关系可近似地用如图(1)中的线段l来表示;1 m2建筑面积上的资金投入Q(万元)与容积率t的关系可近似地用如图(2)中的一段抛物线段c来表示.(Ⅰ)试求图(1)中线段l的函数关系式,并求出开发该小区的用地面积;
(Ⅱ)求出图(2)中抛物线段c的函数关系式.

查看习题详情和答案>>
 ,为充分利用土地资源,更好地解决人们的住房需求,并适当的控制建筑物的高度,一般地容积率t不小于1且不大于8.一房地产开发商在开发某小区时,结合往年开发经验知,建筑面积M(m2)与容积率t的关系可近似地用如图(1)中的线段l来表示;1 m2建筑面积上的资金投入Q(万元)与容积率t的关系可近似地用如图(2)中的一段抛物线段c来表示.
,为充分利用土地资源,更好地解决人们的住房需求,并适当的控制建筑物的高度,一般地容积率t不小于1且不大于8.一房地产开发商在开发某小区时,结合往年开发经验知,建筑面积M(m2)与容积率t的关系可近似地用如图(1)中的线段l来表示;1 m2建筑面积上的资金投入Q(万元)与容积率t的关系可近似地用如图(2)中的一段抛物线段c来表示.
 ,为充分利用土地资源,更好地解决人们的住房需求,并适当的控制建筑物的高度,一般地容积率t不小于1且不大于8.一房地产开发商在开发某小区时,结合往年开发经验知,建筑面积M(m2)与容积率t的关系可近似地用如图(1)中的线段l来表示;1 m2建筑面积上的资金投入Q(万元)与容积率t的关系可近似地用如图(2)中的一段抛物线段c来表示.
,为充分利用土地资源,更好地解决人们的住房需求,并适当的控制建筑物的高度,一般地容积率t不小于1且不大于8.一房地产开发商在开发某小区时,结合往年开发经验知,建筑面积M(m2)与容积率t的关系可近似地用如图(1)中的线段l来表示;1 m2建筑面积上的资金投入Q(万元)与容积率t的关系可近似地用如图(2)中的一段抛物线段c来表示.