摘要: 切割线定理揭示了从圆外一点引圆的切线和割线.切线长和这点到割线与圆的交点的两条线段的长之间的关系.其推论通常又称为割线定理.它和切割线定理的关系非常密切.应用时要注意定理的条件和结论.
网址:http://m.1010jiajiao.com/timu3_id_450215[举报]
圆的切线
[1]定义:和圆有
[2]判定:(1)到圆心的距离等于这个圆的
(2)经过半径
[3]性质:(1)圆的切线
(2)从圆外一点引圆的两条切线,它们的切线长
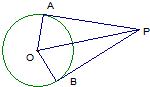
结论:P是⊙O外一点,PA、PB分别切⊙O于A、B,C是弧AB上一点,DE切⊙O于C交PA、PB于D、E,则△PDE的周长为
查看习题详情和答案>>
[1]定义:和圆有
一个交点
一个交点
的直线叫圆的切线.[2]判定:(1)到圆心的距离等于这个圆的
半径
半径
的直线是圆的切线;(2)经过半径
的外端
的外端
并且垂直于
垂直于
这条半径的直线是圆的切线.[3]性质:(1)圆的切线
垂直于
垂直于
过切点
切点
的半径.(2)从圆外一点引圆的两条切线,它们的切线长
相等
相等
,圆心和这个点的连线平分两切线的夹角
两切线的夹角
.(切线长定理)结论:P是⊙O外一点,PA、PB分别切⊙O于A、B,C是弧AB上一点,DE切⊙O于C交PA、PB于D、E,则△PDE的周长为
2PA
2PA
. 如图,一个充气的救生圈.虚线所示的大圆,半径是33厘米.实线所示的小圆,半径是9厘米.有两只蚂蚁同时从A点出发,以同样的速度分别沿大圆和小圆爬行.问:小圆上的蚂蚁爬了几圈后,第一次碰上大圆上的蚂蚁.(思考时间:30秒)
如图,一个充气的救生圈.虚线所示的大圆,半径是33厘米.实线所示的小圆,半径是9厘米.有两只蚂蚁同时从A点出发,以同样的速度分别沿大圆和小圆爬行.问:小圆上的蚂蚁爬了几圈后,第一次碰上大圆上的蚂蚁.(思考时间:30秒)27、小明学习了垂径定理,做了下面的探究,请根据题目要求帮小明完成探究.
(1)更换定理的题设和结论可以得到许多真命题.如图1,在⊙0中,C是劣弧AB的中点,直线CD⊥AB于点E,则AE=BE.请证明此结论;
(2)从圆上任意一点出发的两条弦所组成的折线,成为该圆的一条折弦.如图2,PA,PB组成⊙0的一条折弦.C是劣弧AB的中点,直线CD⊥PA于点E,则AE=PE+PB.可以通过延长DB、AP相交于点F,再连接AD证明结论成立.请写出证明过程;
(3)如图3,PA.PB组成⊙0的一条折弦,若C是优弧AB的中点,直线CD⊥PA于点E,则AE,PE与PB之间存在怎样的数量关系?写出结论,不必证明.

查看习题详情和答案>>
(1)更换定理的题设和结论可以得到许多真命题.如图1,在⊙0中,C是劣弧AB的中点,直线CD⊥AB于点E,则AE=BE.请证明此结论;
(2)从圆上任意一点出发的两条弦所组成的折线,成为该圆的一条折弦.如图2,PA,PB组成⊙0的一条折弦.C是劣弧AB的中点,直线CD⊥PA于点E,则AE=PE+PB.可以通过延长DB、AP相交于点F,再连接AD证明结论成立.请写出证明过程;
(3)如图3,PA.PB组成⊙0的一条折弦,若C是优弧AB的中点,直线CD⊥PA于点E,则AE,PE与PB之间存在怎样的数量关系?写出结论,不必证明.

 30、如图,AB是⊙O的弦,从圆上任意一点作弦CD⊥AB,作∠OCD的平分线交⊙O于点P,若AP=5,则BP的值为( )
30、如图,AB是⊙O的弦,从圆上任意一点作弦CD⊥AB,作∠OCD的平分线交⊙O于点P,若AP=5,则BP的值为( )