摘要: 讲过切线长定理以后.已知一条切线时.通常有如下五个性质可用: (1)切线和圆有且只有一个公共点, (2)切线和圆心的距离等于该圆的半径, (3)切线垂直于过切点的半径, (4)经过圆心垂直于切线的直线必过切点, (5)经过切点垂直于切线的直线必过圆心. 若已知一个圆的两条切线相交.则又多了“切线长相等 的性质, 若已知一个圆的两条切线互相平行.则可得出“圆上两个切点的连线为直径 的性质.
网址:http://m.1010jiajiao.com/timu3_id_450211[举报]
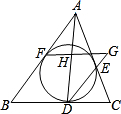 如图,△ABC的内切圆分别切BC、CA、AB于点D、E、F,过点F作BC的平行线分别交直线DA、DE于点H、G.问:图中除由切线长定理可知AF=AE,BF=BD,CD=CE外,还有相等的线段吗?若有,请指出来,并加以证明.
查看习题详情和答案>>
如图,△ABC的内切圆分别切BC、CA、AB于点D、E、F,过点F作BC的平行线分别交直线DA、DE于点H、G.问:图中除由切线长定理可知AF=AE,BF=BD,CD=CE外,还有相等的线段吗?若有,请指出来,并加以证明.
查看习题详情和答案>>
圆的切线
[1]定义:和圆有
[2]判定:(1)到圆心的距离等于这个圆的
(2)经过半径
[3]性质:(1)圆的切线
(2)从圆外一点引圆的两条切线,它们的切线长
结论:P是⊙O外一点,PA、PB分别切⊙O于A、B,C是弧AB上一点,DE切⊙O于C交PA、PB于D、E,则△PDE的周长为
查看习题详情和答案>>
[1]定义:和圆有
一个交点
一个交点
的直线叫圆的切线.[2]判定:(1)到圆心的距离等于这个圆的
半径
半径
的直线是圆的切线;(2)经过半径
的外端
的外端
并且垂直于
垂直于
这条半径的直线是圆的切线.[3]性质:(1)圆的切线
垂直于
垂直于
过切点
切点
的半径.(2)从圆外一点引圆的两条切线,它们的切线长
相等
相等
,圆心和这个点的连线平分两切线的夹角
两切线的夹角
.(切线长定理)结论:P是⊙O外一点,PA、PB分别切⊙O于A、B,C是弧AB上一点,DE切⊙O于C交PA、PB于D、E,则△PDE的周长为
2PA
2PA
.如图,△ABC的内切圆分别切BC、CA、AB于点D、E、F,过点F作BC的平行线分别交直线DA、DE于点H、G.问:图中除由切线长定理可知AF=AE,BF=BD,CD=CE外,还有相等的线段吗?若有,请指出来,并加以证明.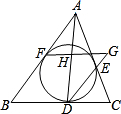
查看习题详情和答案>>

 如图,△ABC的内切圆分别切BC、CA、AB于点D、E、F,过点F作BC的平行线分别交直线DA、DE于点H、G.问:图中除由切线长定理可知AF=AE,BF=BD,CD=CE外,还有相等的线段吗?若有,请指出来,并加以证明.
如图,△ABC的内切圆分别切BC、CA、AB于点D、E、F,过点F作BC的平行线分别交直线DA、DE于点H、G.问:图中除由切线长定理可知AF=AE,BF=BD,CD=CE外,还有相等的线段吗?若有,请指出来,并加以证明.