摘要：14．非空集合G关于运算满足:(1)对任意.都有,(2)存在.使得对一切.都有.则称G关于运算为“融洽集 .现给出下列集合和运算: ①G={非负整数}.为整数的加法, ②G={偶数}.为整数的乘法, ③G＝{平面向量}.为平面向量的加法, ④G={二次三项式}.为复数的乘法, ⑤G={虚数}.为复数的乘法, 其中G关于运算为“融洽集 的是 .(写出所有“融洽集 的序号)
网址：http://m.1010jiajiao.com/timu3_id_4468321[举报]
16、非空集合G关于运算⊕满足：①对于任意a、b∈G，都有a⊕b∈G；②存在e∈G，使对一切a∈G都有a⊕e=e⊕a=a，则称G关于运算⊕为和谐集，现有下列命题：
①G={a+bi|a，b为偶数}，⊕为复数的乘法，则G为和谐集；
②G={二次三项式}，⊕为多项式的加法，则G不是 和谐集；
③若⊕为实数的加法，G⊆R且G为和谐集，则G要么为0，要么为无限集；
④若⊕为实数的乘法，G⊆R且G为和谐集，则G要么为0，要么为无限集，其中正确的有
查看习题详情和答案>>
①G={a+bi|a，b为偶数}，⊕为复数的乘法，则G为和谐集；
②G={二次三项式}，⊕为多项式的加法，则G不是 和谐集；
③若⊕为实数的加法，G⊆R且G为和谐集，则G要么为0，要么为无限集；
④若⊕为实数的乘法，G⊆R且G为和谐集，则G要么为0，要么为无限集，其中正确的有
②③
．非空集合G关于运算满足：①对于任意a、b∈G，都有a?b∈G；②存在e∈G，使对一切a∈G都有a?e=e?a=a，则称G关于运算为融洽集，现有下列集合运算：
（1）G={非负整数}，为整数的加法；
（2）G={偶数}，为整数的乘法；
（3）G={平面向量}，为平面向量的加法；
（4）G={二次三项式}，为多项式的加法；
其中关于运算的融洽集有
查看习题详情和答案>>
（1）G={非负整数}，为整数的加法；
（2）G={偶数}，为整数的乘法；
（3）G={平面向量}，为平面向量的加法；
（4）G={二次三项式}，为多项式的加法；
其中关于运算的融洽集有
（1）（3）
（1）（3）
．非空集合G关于运算
满足：①对于任意a、b
G，都有abG；②存在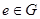
，使对一切
都有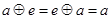
，则称G关于运算为和谐集，现有下列命题：
①G={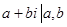 
为偶数}，为复数的乘法，则G为和谐集。
②G={二次三项式}，为多项式的加法，则G不是和谐集。
③若为实数的加法，G 
且G为和谐集，则G要么为
，要么为无限集。
④若为实数的乘法，G 且G为和谐集，则G要么为，要么为无限集。
其中正确的有____________。
查看习题详情和答案>>
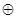满足：①对于任意a、b
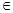G，都有a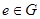
，使对一切
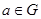都有a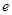
=