摘要：24．对于函数f(x).若存在x0∈R.使f(x0)=x0成立.则称x0为f(x)的不动点.已知函数f(x)=ax2+. (1)当a=1,b=-2时.求函数f(x)的不动点, (2)若对任意实数b.函数f(x)恒有两个相异的不动点.求a的取值范围, 的条件下.若y=f(x)图象上A.B两点的横坐标是函数f(x)的不动点.且A.B两点关于直线y=kx+1/(2a2+1)对称.求b的最小值.
网址：http://m.1010jiajiao.com/timu3_id_4461241[举报]
对于函数f(x)，若存在x0∈R，使f(x0)＝x0成立，则称x0为f(x)的不动点．如果函数
f(x)＝ax2＋bx＋1(a＞0)有两个相异的不动点x1，x2．
⑴若x1<1<x2，且f(x)的图象关于直线x＝m对称，求证：
<m<1；
⑵若|x1|<2且|x1－x2|＝2，求b的取值范围．
查看习题详情和答案>>对于函数f(x)，若存在x0∈R，使f(x0)＝x0成立，则称x0为f(x)的不动点，已知函数f(x)＝ax2＋(b＋1)x＋b－1(a≠0)．
(1)当a＝1，b＝－2时，求f(x)的不动点；
(2)若对任意实数b，函数f(x)恒有两个相异的不动点，求a的取值范围．
对于函数f(x)，若存在x0∈R，使f(x0)＝x0成立，则称x0为f(x)的不动点．如果函数
f(x)＝ax2＋bx＋1(a＞0)有两个相异的不动点x1，x2．
⑴若x1<1<x2，且f(x)的图象关于直线x＝m对称，求证：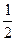
<m<1；
⑵若|x1|<2且|x1－x2|＝2，求b的取值范围．
f(x)＝ax2＋bx＋1(a＞0)有两个相异的不动点x1，x2．
⑴若x1<1<x2，且f(x)的图象关于直线x＝m对称，求证：
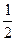<m<1；⑵若|x1|<2且|x1－x2|＝2，求b的取值范围．
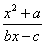(b，c∈N)有且只有两个不动点0，2，且f(-2)＜
，
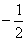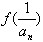=1(Sn为数列前n项和)，求数列{an}的通项公式an；