摘要:某班数学兴趣小组有男生和女生各3名.现从中任选2名学生去参加校数学竞赛.求: (I)恰有一名参赛学生是男生的概率, (II)至少有一名参赛学生是男生的概率, (Ⅲ)至多有一名参赛学生是男生的概率. 已知向量=(cos.sin).=(cos.-sin).且x∈[.]. (I)求及, =-的最小值. 设f(x)=ax2+bx+c的导数为f∕|=1. f∕=0. 的解析式, (II)对于任意的x1,x2∈[0.1].且x1≠x2. 求证:|f(x2)-f(x1)|≤2|x2-x1|与|f(x2)-f(x1)|≤1都成立. 如图为一几何体的展开图: (I)沿图中虚线将它们折叠起来.是哪一种特殊几何体?并请画出其直观图.比例尺是, (II)需要多少个这样的几何体才能拼成一个棱长为6cm的正方体ABCD-A1B1C1D1.请画出其示意图(需在示意图中分别表示出这种几何体), (Ⅲ)设正方体ABCD-A1B1C1D1的棱CC1的中点为E.试求:异面直线EB与AB1所成角的余弦值及平面AB1E与平面ABC所成二面角的余弦值. 已知:f(x)=的反函数为g(x),点An(an,)在曲线y=g(x)上(n∈N+).且a1=1. 的表达式, (II)证明数列{}为等差数列, (Ⅲ)求数列{an}的通项公式, (Ⅳ)设bn=,记Sn=b1+b2+--+bn.求Sn. 已知动圆与圆F1:x2+y2+6x+4=0和圆F2:x2+y2-6x-36=0都外切. (I)求动圆圆心的轨迹C的方程, (II)若直线L被轨迹C所截得的线段的中点坐标为.求直线L的方程, (Ⅲ)若点P在直线L上.且过点P的椭圆C∕以轨迹C的焦点为焦点.试求点P在什么位置时.椭圆C∕的长轴最短.并求出这个具有最短长轴的椭圆C∕的方程.
网址:http://m.1010jiajiao.com/timu3_id_4461110[举报]
(本小题满分12分)
某校高三(1)班共有 名学生,他们每天自主学习的时间全部在
名学生,他们每天自主学习的时间全部在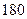 分钟到
分钟到 分钟之间,按他们学习时间的长短分
分钟之间,按他们学习时间的长短分 个组统计得到如下频率分布表:
个组统计得到如下频率分布表:
| 分组 | 频数 | 频率 |
| [180 , 210) |  |  |
| [210 , 240) |  |  |
| [240 , 270) |  |  |
| [270 , 300) |  |  |
| [300 , 330) |  |  |
 ,
, 的值;
的值;(2)某兴趣小组为研究每天自主学习的时间与学习成绩的相关性,需要在这
 名学生中按时间用分层抽样的方法抽取
名学生中按时间用分层抽样的方法抽取 名学生进行研究,问应抽取多少名第一组的学生?
名学生进行研究,问应抽取多少名第一组的学生?(3)已知第一组的学生中男、女生均为
 人.在(2)的条件下抽取第一组的学生,求既有男生又有女生被抽中的概率.
查看习题详情和答案>>
人.在(2)的条件下抽取第一组的学生,求既有男生又有女生被抽中的概率.
查看习题详情和答案>>
(本小题满分12分)
某校高三(1)班共有![]() 名学生,他们每天自主学习的时间全部在
名学生,他们每天自主学习的时间全部在![]() 分钟到
分钟到![]() 分钟之间,按他们学习时间的长短分
分钟之间,按他们学习时间的长短分![]() 个组统计得到如下频率分布表:
个组统计得到如下频率分布表:
| 分组 | 频数 | 频率 |
| [180 , 210) |
|
|
| [210 , 240) |
|
|
| [240 , 270) |
|
|
| [270 , 300) |
|
|
| [300 , 330) |
|
|
(1)求分布表中![]() ,
,![]() 的值;
的值;
(2)某兴趣小组为研究每天自主学习的时间与学习成绩的相关性,需要在这![]() 名学生中按时间用分层抽样的方法抽取
名学生中按时间用分层抽样的方法抽取![]() 名学生进行研究,问应抽取多少名第一组的学生?
名学生进行研究,问应抽取多少名第一组的学生?
(3)已知第一组的学生中男、女生均为![]() 人.在(2)的条件下抽取第一组的学生,求既有男生又有女生被抽中的概率.
人.在(2)的条件下抽取第一组的学生,求既有男生又有女生被抽中的概率.
 名学生,他们每天自主学习的时间全部在
名学生,他们每天自主学习的时间全部在 分钟到
分钟到 分钟之间,按他们学习时间的长短分
分钟之间,按他们学习时间的长短分 个组统计得到如下频率分布表:
个组统计得到如下频率分布表: 
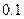








 名学生进行研究,问应抽取多少名第一组的学生?
名学生进行研究,问应抽取多少名第一组的学生? 人.在(2)的条件下抽取第一组的学生,求既有男生又有女生被抽中的概率.
人.在(2)的条件下抽取第一组的学生,求既有男生又有女生被抽中的概率.