0 445717 445725 445731 445735 445741 445743 445747 445753 445755 445761 445767 445771 445773 445777 445783 445785 445791 445795 445797 445801 445803 445807 445809 445811 445812 445813 445815 445816 445817 445819 445821 445825 445827 445831 445833 445837 445843 445845 445851 445855 445857 445861 445867 445873 445875 445881 445885 445887 445893 445897 445903 445911 447348
 都在函数
都在函数 的图象上
的图象上
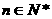
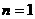 时,
时,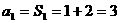 ------------------ 2分
------------------ 2分 时,
时,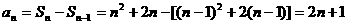 (*)------- 3分
(*)------- 3分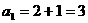 ,也满足(*)式
,也满足(*)式
 的通项公式是
的通项公式是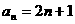 . -------------- 4分
. -------------- 4分

 -------------
------ 6分
-------------
------ 6分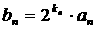
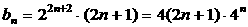 -------------- 7分
-------------- 7分
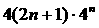 ① 由①
① 由①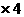 可得
可得
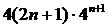 ②
②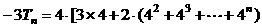
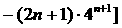
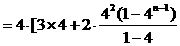
 -------------- 9分
-------------- 9分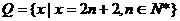 ,
,
 --------------------------- 10分
--------------------------- 10分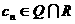 ,其中
,其中 是
是 中的最小数,
中的最小数,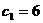 , --------------------------- 11分
, --------------------------- 11分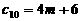
 (
(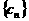 的公差是4 的倍数!)
的公差是4 的倍数!)
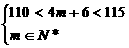 解得
解得
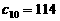 --------------------------- 12分
--------------------------- 12分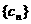 的公差为
的公差为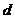
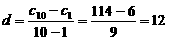

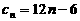 . -------------------------- 14分
. -------------------------- 14分 函数
函数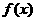 的图象关于原点对称
的图象关于原点对称 对任意实数
对任意实数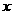 ,有
,有
 …………………………………3分
…………………………………3分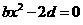 恒成立
恒成立
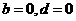
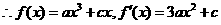
 时,
时,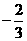 ,
, 且
且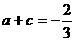 ,
,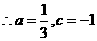 …………………………………………………………………………5分
…………………………………………………………………………5分 时,图象上不存在这样的两点使结论成立。
时,图象上不存在这样的两点使结论成立。 ,使得过此两点处的切线互相垂直,则由
,使得过此两点处的切线互相垂直,则由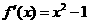 知两点处的切线斜率分别为
知两点处的切线斜率分别为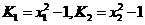 …………………………………………… …6分
…………………………………………… …6分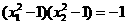 (*)
(*)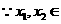 [-1,1]
[-1,1] 与(*)矛盾………………………………9分
与(*)矛盾………………………………9分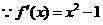 令
令 得
得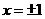 ,
,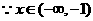
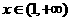 时,
时,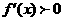 ,
,
 时
时
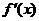 在[-1,1]上是减函数,且
在[-1,1]上是减函数,且 …………………………11分
…………………………11分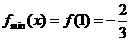
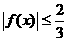
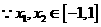 时,
时,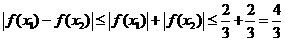 ………………14分
………………14分 项和为
项和为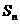 ,对一切正整数
,对一切正整数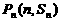 都在函数
都在函数 .
. ,求数列
,求数列 的前
的前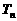 ;
;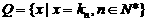 ,
, ,等差数列
,等差数列 的任一项
的任一项 ,其中
,其中 中的最小数,
中的最小数,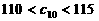 ,求
,求 =(cos
=(cos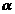 -3, sin
-3, sin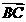 =(cos
=(cos 。
。 。………………………4分
。………………………4分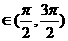 ,∴
,∴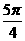 ……6分
……6分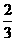 .① ………………………………………………8分
.① ………………………………………………8分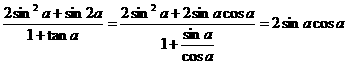 .
.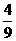 , ∴2sin
, ∴2sin , ………12分
, ………12分  ………………………………………………13分
………………………………………………13分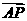 =(x,y-1),
=(x,y-1), =(x,y+1),
=(x,y+1), =(1-x,-y)
=(1-x,-y) ,
,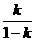 ,0)为圆心,以
,0)为圆心,以 为半径的圆。
为半径的圆。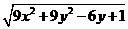 。又x2+y2=4x-3,
。又x2+y2=4x-3,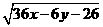 ∵(x-2)2+y2=1,∴令x=2+cosθ,y=sinθ。
∵(x-2)2+y2=1,∴令x=2+cosθ,y=sinθ。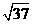 cos(θ+φ)+46∈[46-6
cos(θ+φ)+46∈[46-6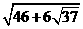 =3+
=3+ =
= .
. ----------------------- 4分
----------------------- 4分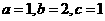
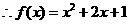 ----------------------- 6分
----------------------- 6分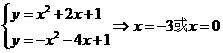 ------------------- 8分
------------------- 8分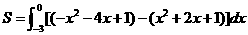 ------------------- 10分
------------------- 10分
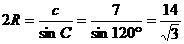 ,…………………………3分
,…………………………3分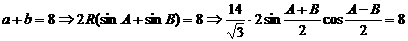 …7分
…7分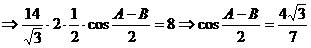 ………………………10分
………………………10分 ………………………………………12分
………………………………………12分 14 :5
14 :5