摘要:20.设函数.R). (1)若.过两点(0.0).(.0)的中点作与轴垂直的直线.与函数的图象交于点.求证:函数在点P处的切线过点(.0). (2)若).且当时恒成立.求实数的取值范围. 解(1)由已知 ----1分 ----2分 所求.所求切线斜率为 ----3分 切线方程为 所以.函数y=f (x)过点P的切线过点(b,0) ----4分 (2)因为.所以. ----5分 当时.函数上单调递增.在(.)单调递减. 在上单调递增. 所以.根据题意有 即 解之得.结合.所以 ----8分 当时.函数单调递增. ----9分 所以.根据题意有 ----10分 即. 整理得() 令. .所以“ 不等式无解.-13分 综上可知:. ----14分
网址:http://m.1010jiajiao.com/timu3_id_4458618[举报]
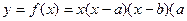 、
、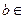 R)。
R)。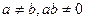 ,过两点(0,0)、(
,过两点(0,0)、(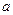 ,0)的中点作与
,0)的中点作与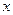 轴垂直的直线,与函数
轴垂直的直线,与函数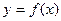 的图象交于点
的图象交于点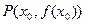 ,求证:函数
,求证:函数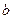 ,0)。
,0)。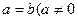 ),且当
),且当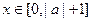 时
时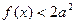 恒成立,求实数
恒成立,求实数