摘要:如图.四边形ABCD是边长为2的正方形.PA⊥平面ABCD.DE//PA.PA=2DE=AB.F为PC的中点. (1)求证:EF//平面ABCD, (2)求平面PCE与平面ABCD所成二面角的余弦值, (3)求点A到平面PEC的距离. (1)证法一:取PA中点G′连接EG′.FG′.AC 易得EG′//AD.FG′//AC ------2分 ∴平面EFG′//平面ABCD ∴EF//平面ABCD ----4分 证法二:由条件知DC.DA.DE两两垂直. ∴以DC.DA.DE所在直线为坐标轴建立空间直角坐标系D-xyz 则A.C D.P ∵F这PC的中点 ∴F ∵ --2分 即 又∵而ABCD 而EF面ABCD ∴EF//面ABCD ----4分 (2)解法1 延长PE.AD交于G点.连接GC. 则平面PEC∩平面ABCD=GC ∵ ∴GD=DA=DC ∴△ACG为直角三角形 ∴GC⊥AC 而AC为PC在平面ABCD内的射影.GC平面ABCD ∴由三垂线定理得GC⊥PC ∴∠PCA就是平面PEC与平面ABCD所成二面角的平面角 ----6分 在Rt△PCA中. ----8分 解法2 设平面PEC的法向量 ∴ ∴ ----6分 又DE⊥平面ABCD. 即是平面ABCD的法向量.且= ||=1.设平面PEC与平面ABCD的二面角为θ 则 ----8分 (3)解法1 作AH⊥PC于H点 由EF//DB.AC⊥DB.PA⊥平面ABCD.PA⊥BD.且AC∩PA=A ∴BD⊥平面PAC ∴EF⊥平面PAC 而AH平面PAC ∴AH⊥EF 又AH⊥PC EF∩PC=F ∴AH⊥平面PEC 即AH为点A到平面PEC的距离 故在Rt△PCA中有 ----12分 解法2 由(2)知平面PEC的法向量为n=() 且|n|= ∴A到平面的距离 ----
网址:http://m.1010jiajiao.com/timu3_id_4458616[举报]
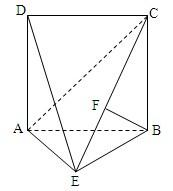 如图,四边形ABCD是边长为2的正方形,△ABE为等腰三角形,AE=BE,平面ABCD⊥平面ABE,点F在CE上,且BF⊥平面ACE.
如图,四边形ABCD是边长为2的正方形,△ABE为等腰三角形,AE=BE,平面ABCD⊥平面ABE,点F在CE上,且BF⊥平面ACE.(Ⅰ)判断平面ADE与平面BCE是否垂直,并说明理由;
(Ⅱ)求点D到平面ACE的距离. 查看习题详情和答案>>
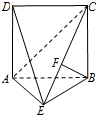 如图,四边形ABCD是边长为2的正方形,△ABE为等腰三角形,AE=BE,平面ABCD⊥平面ABE,点F在CE上,且BF⊥平面ACE.
如图,四边形ABCD是边长为2的正方形,△ABE为等腰三角形,AE=BE,平面ABCD⊥平面ABE,点F在CE上,且BF⊥平面ACE.(Ⅰ)证明:平面ADE⊥平面BCE;
(Ⅱ)求点D到平面ACE的距离.
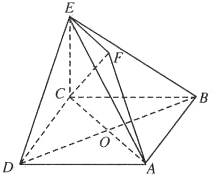 如图,四边形ABCD是边长为
如图,四边形ABCD是边长为| 2 |
(1)求证:AF∥平面BDE;
(2)求证:CF⊥平面BDE;
(3)求二面角A-BE-D的大小.
 如图,四边形ABCD是边长为2的正方形,△ABE为等腰三角形,AE=BE,平面ABCD⊥平面ABE,点F在CE上,且BF⊥平面ACE.
如图,四边形ABCD是边长为2的正方形,△ABE为等腰三角形,AE=BE,平面ABCD⊥平面ABE,点F在CE上,且BF⊥平面ACE.