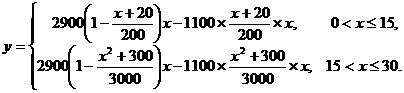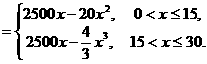文16.(本小题满分12分)
已知 ,
,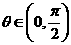 ,求
,求 和
和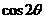 的值.
的值.
[考查目标]本小题主要考查三角函数的诱导公式及和(差)角公式等基础知识,
考查运算能力.
[答卷分析] 平均分:10.11 难度:0.84 标准差:3.74
[本题别解主要有]
别解: 令 ,则r=5k,y=3k
(k>0) .又由
,则r=5k,y=3k
(k>0) .又由 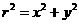 得:x=±4k,
得:x=±4k,
而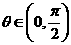 ,所以x=4k .
,所以x=4k .  .
.
[本题出现的典型错误有]
① 公式记错,
例如 等.
等.
② 应用万能公式,但公式记不牢.
理16. (本小题满分12分)
已知 .
.
(Ⅰ)求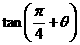 的值;
的值;
(Ⅱ)求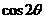 的值.
的值.
[考查目标]本小题主要考查三角函数的诱导公式及和(差)角公式等基础知识,
考查运算能力.
[命题溯源]《第三册》(选修Ⅱ)P125.练习1(1)改编.
[本题别解主要有]
别解一: 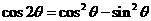

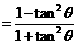
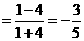
别解二:
 ,
,
又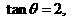 可知
可知 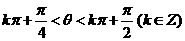 , 从
, 从
∴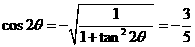 .
.
[答卷分析] 平均分:9.55 难度:0.80 标准差:3.71
[本题出现的典型错误有]
① 
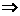
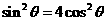
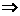
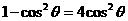
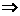

从而 (重复平方)
(重复平方)
② 由 ,则:
,则: , 知
, 知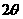 可在第二或四象限.
可在第二或四象限.
当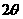 在第二:
在第二: ; 当
; 当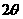 在第四:
在第四: .
.
 文17.(本小题满分14分)
文17.(本小题满分14分)
如图6所示,在长方体 中,
中,
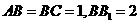 ,连结
,连结 、
、 .
.
(Ⅰ)求证:
 ;
;
(Ⅱ)求三棱锥 的体积. 图6
的体积. 图6
[考查目标]本小题主要考查空间线面关系,考查空间想象能力和推理运算能力.
[答卷分析] 平均分:10.11 难度:0.73 标准差:4.75
[本题别解主要有]
① 用三垂线定理证明(略);
② 先证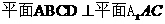
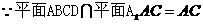 ,正方形ABCD中,
,正方形ABCD中,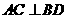 ,
,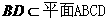

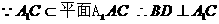
③ 向量法.
以A为原点,AB、AD、AA1所在直线分别为x轴、y轴建立空间直角坐标系,
则B(1,0,0),D(0,1,0) ,A1((0,0,2),C(1,1,0) .
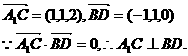
[本题出现的典型错误有]
① 叙述不规范:如“ ”写成“
”写成“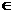 ”等;
”等;
② 建立直角坐标系,但叙述不完整,或图形上不标方向;
③ 书写不规范;
④ 用等积法求,但找错高,常把OC当作三棱锥 的高;
的高;
⑤ 计算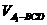 时,将
时,将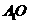 作为三棱锥
作为三棱锥 的高;
的高;
⑥ 计算出错.
理17. (本小题满分14分)
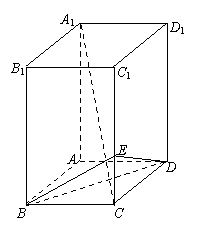 如图5所示,在长方体
如图5所示,在长方体 中,
中,
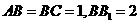 ,
,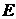 是棱
是棱 上的点,
上的点,
且 .
.
(Ⅰ)求三棱锥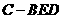 的体积;
的体积;
(Ⅱ)求证: 平面
平面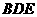 .
.
[考查目标]本小题主要考查空间线面关系,考查空间想象能
力和推理运算能力.
[答卷分析] 平均分:11.60 难度:0.80 标准差:3.41.
[本题别解主要有]
别解:(Ⅰ)平面BDE的法向量 ,
,
点C到平面BDE的距离d=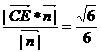 ,SBDE=
,SBDE= ,再计算体积.
,再计算体积.
(Ⅱ)∵ ∴
∴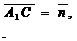
∴ ∴AC⊥平面BDE.
∴AC⊥平面BDE.
[本题出现的典型错误有]
① 第(Ⅰ)问,没有交待高CE扣1分 ;
② 第(Ⅱ)问,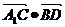 和
和 的运算过程没有造成扣分;
的运算过程没有造成扣分;
③ 向量垂直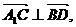
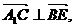 没有转化为直线垂直A1C⊥BD, A1C⊥BE造成扣分.
没有转化为直线垂直A1C⊥BD, A1C⊥BE造成扣分.
④ 体积公式记错, 如 ,
,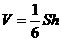 等.
等.
文18.(本小题满分14分)
函数 和
和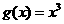 的图像的示意图如图7所示,
的图像的示意图如图7所示,
设两函数的图像交于点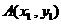 ,
,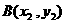 ,且
,且 .
.
 (Ⅰ)请指出示意图中曲线
(Ⅰ)请指出示意图中曲线 ,
,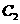 分别对应哪一个函数?
分别对应哪一个函数?
(Ⅱ)若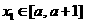 ,
,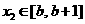 ,且
,且
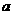
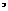
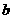
 ,
,
指出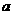 ,
,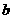 的值,并说明理由;
的值,并说明理由;
(Ⅲ)结合函数图像的示意图,判断 ,
,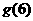 ,
, ,
,
 的大小,并按从小到大的顺序排列.
的大小,并按从小到大的顺序排列.
[考查目标]本小题主要考查空间线面关系,考查空间想象能力和推理运算能力.
[答卷分析] 平均分:6.49 难度:0.46 标准差:3.79
[本题别解主要有]观察下表可以得到解答:
|
x |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
G(x) |
1 |
8 |
17 |
64 |
125 |
216 |
343 |
512 |
729 |
100 |
|
F(x) |
2 |
4 |
8 |
16 |
32 |
64 |
128 |
256 |
512 |
1024 |
[本题出现的典型错误有]
(1) 
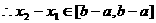
∴ a=1 , b=6
∵ f(x)=g(x),
 ,符合题意
,符合题意
∵
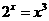 ,∴
,∴ 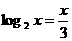
∴
当x=1时,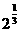 离等于
离等于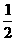 的机会较小;当x=2时,
的机会较小;当x=2时,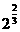 离等于2的机会较大;
离等于2的机会较大;
当x=3时, 离等于3的机会较大;……
离等于3的机会较大;……
当x=10时,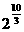 离等于10的机会较大;当x=12时,
离等于10的机会较大;当x=12时, 离等于12的机会较小;
离等于12的机会较小;
∴
综上所述,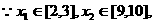 ∴ a=2,b=9
∴ a=2,b=9
令F(x)= , ∵x∈[1,3],根据二分法得,F(1)>0,F(2)<0, ∴a=1.
, ∵x∈[1,3],根据二分法得,F(1)>0,F(2)<0, ∴a=1.
(2) 函数符号表达不清楚;
(3) 得分点把握不到位:如
① 计算出f(6)与g(6)的值,但没有结论f(6)<g(6)
②f(2007)与g(2007)的比较说理不清楚或者没有说理过程
(4) 对“a=1,b=9”的理解不清,不会将问题进行转化,审题缺乏灵活性.
理18. (本小题满分12分)
甲箱的产品中有5个正品和3个次品, 乙箱的产品中有4个正品和3个次品.
(Ⅰ)从甲箱中任取2个产品,求这2个产品都是次品的概率;
(Ⅱ)若从甲箱中任取2个产品放入乙箱中, 然后再从乙箱中任取一个产品,求取出的这个产品是正品的概率.
[考查目标]本小题主要考查条件概率和互斥事件的概率计算,考查运用概率知识解决实
际问题能力.
[答卷分析] 平均分:7.65 难度:0.64 标准差:3.81
[本题别解主要有]
别解1:分3类,然后相加而得,解法如下:
记“从甲箱中取出2个产品为正品放入乙箱,然后再从乙箱中取出正品”为事件A,
则P(A)=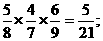
记“从甲箱中取出2个产品为一个正品和一个次品放入乙箱,然后再从乙箱中取出正品”
为事件B,则P(B)=
记“从甲箱中取出2个产品为次品放入乙箱,然后再从乙箱中取出正品”为事件C,
则P(C)=
记“从乙箱中取出的产品为正品”为事件D,则A、B、C互斥,且D=A+B+C,
所以,P(D)=P(A+B+C)=  +
+  +
+  =
= 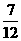
别解2:设从甲箱中取了2个产品放入乙箱后,乙箱中的正品数为X,则X的取值可能为4,
5,6,其中
X=4”表示“从甲箱中取出2个产品为次品放入乙箱”,则P(X=4)=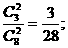
“X=5”表示“从甲箱中取出2个产品为一个正品和一个次品放入乙箱”,
则P(X=5)=
“X=6”表示“从甲箱中取出2个产品为2个正品放入乙箱”,则P(X=6)=
所以,乙箱中正品数X的期望为 E(X)=
所以,此时从乙箱中再取出一个产品为正品的概率为P = 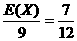
别解3:(Ⅱ)用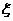 表示从甲箱中取出正品数,则
表示从甲箱中取出正品数,则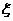 的分布列为:
的分布列为:
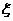 |
0 |
1 |
2 |
|
P |
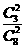 |
 |
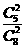 |
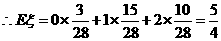
故从乙箱中取出一个产品是正品的概率为P= .
.
[本题出现的典型错误有]
(1) 概念不清晰
② 学生对条件概率,互斥事件等基本慨念不清楚;
②甚至有的学生出现 等明显问题,体现出学生基本慨念的薄弱;
等明显问题,体现出学生基本慨念的薄弱;
③少数学生还出现 这样的形式.
这样的形式.
(2) 计算不准确
①组合数计算 =
=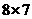 =56等低级错误;
=56等低级错误;
②分数相加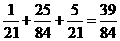 等.
等.
(3) 答题不规范
①没有必要的文字说明;
③
运算结果不追求最简,如: 等不化简;
等不化简;
③ 第2问很多只考虑了“乙箱中取到正品”的概率,而未注意“甲箱中取来的正品”
产生的影响;
④ 忘记作答,扣1分.
文19.(本小题满分12分)
某工厂日生产某种产品最多不超过30件,且在生产过程中次品率 与日产量
与日产量 (
(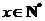 )
)
件间的关系为
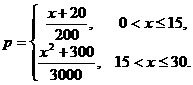
每生产一件正品盈利2900元,每出现一件次品亏损1100元.
(Ⅰ)将日利润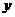 (元)表示为日产量
(元)表示为日产量 (件)的函数;
(件)的函数;
(Ⅱ)该厂的日产量为多少件时,日利润最大?
(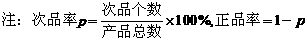 )
)
[考查目标]本小题主要考查函数和导数的应用,考查综合运用数学知识分析问题与解决实际问题的能力.
[答卷分析] 平均分:1.80 难度:0.15 标准差:2.97
[本题出现的典型错误有]
1. 最大问题是计算问题:
① 列出表达式化简错误;
② 求最大值计算不正确. 如:
(a)当在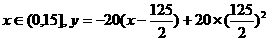
学生知道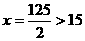 超出x的范围,但都没有明确交待就直接在x=15处取得最大值3300元
超出x的范围,但都没有明确交待就直接在x=15处取得最大值3300元
(b)当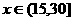 时,会求导得x=25时,y’=0,但没有明确单调性,直接在x=25时取最大值.
时,会求导得x=25时,y’=0,但没有明确单调性,直接在x=25时取最大值.
(c)没有比较两段函数的最大值.
3.数学成绩前十名
一模(由市招考办提供)
理科 文科
|
姓名 |
成绩 |
学校 |
|
吴洋 |
144 |
番禺中学 |
|
王妍 |
143 |
省实 |
|
江宝灿 |
141 |
广雅 |
|
佘纲正 |
141 |
2中 |
|
刘俊生 |
141 |
5中 |
|
卢晓丹 |
141 |
6中 |
|
戴浩斌 |
141 |
6中 |
|
谭丽琼 |
140 |
省实 |
|
张影岚 |
140 |
省实 |
|
周浩杰 |
140 |
2中 |
|
李文姗 |
140 |
2中 |
|
李倩华 |
140 |
6中 |
|
伍锦标 |
140 |
华附 |
|
肖妍琳 |
140 |
华附 |
|
刘芷艺 |
140 |
47中 |
|
唐敏 |
140 |
其他 |
|
刘惠花 |
140 |
从化中学 |
|
姓名 |
成绩 |
学校 |
|
叶键民 |
147 |
华附 |
|
简必希 |
145 |
省实 |
|
谢龙 |
145 |
执信 |
|
颜晖皓 |
145 |
仲元 |
|
杨永铿 |
145 |
3中 |
|
程家豪 |
144 |
广雅 |
|
黎丹 |
144 |
省实 |
|
李浩麟 |
144 |
7中 |
|
潘文 |
144 |
执信 |
|
黄浩斌 |
143 |
广雅 |
|
陈腾泓 |
143 |
华附 |
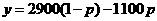 ,漏乘x,化简后得:
,漏乘x,化简后得:
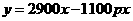 ,把正品数当成x;
,把正品数当成x; ,对“100%”理解错,多乘100或10.
,对“100%”理解错,多乘100或10.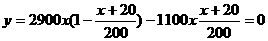 .
.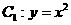 与曲线
与曲线 交于点
交于点 、
、 ,
,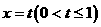 与曲线
与曲线 、
、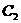 分别相交于点
分别相交于点 、
、 ,连结
,连结
 .
.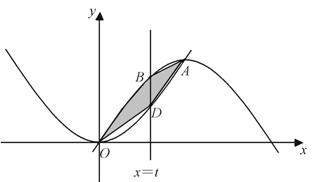 (Ⅰ)写出曲边四边形
(Ⅰ)写出曲边四边形  (阴影部分)的面积
(阴影部分)的面积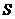 与
与 的函数关系式
的函数关系式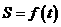 ;
;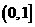 上的最大值.
上的最大值.
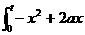 ”的情形经常出现,有些就干脆不写积分符号,直接写“
”的情形经常出现,有些就干脆不写积分符号,直接写“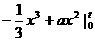 ”
”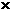 高,即
高,即 与1”的关系进行讨论,而默认为“
与1”的关系进行讨论,而默认为“ 时错误很多;
时错误很多;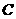 :
: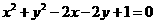 ,直线
,直线 :
: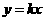 ,且
,且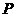 、
、 两点,点
两点,点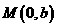 ,且
,且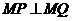 .
. 时,求
时,求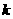 的值;
的值;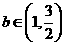 ,求
,求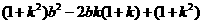

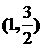 上
上


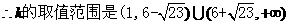

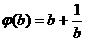 的单调性判断没有过程,或用极端情况代替一般情况:
的单调性判断没有过程,或用极端情况代替一般情况: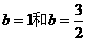 来代替所有情况;
来代替所有情况;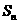 是数列
是数列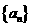 的前
的前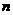 项和,对任意
项和,对任意 N
N 总有
总有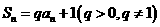 ,
,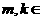 N
N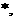 且
且 .
. ;
; 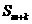 与
与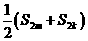 的大小;
的大小;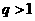 时,试比较
时,试比较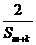 与
与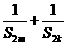 的大小.
的大小.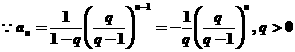
 .
.
 .
.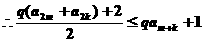 .
. .
.
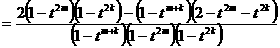
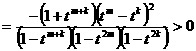 .
. 中第二个加号错了;
中第二个加号错了; ;
; ;
;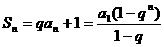 ;
;
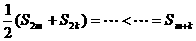 ”的过程中运用了基本不等式,但只考虑了
”的过程中运用了基本不等式,但只考虑了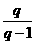 >0的情形.
>0的情形. 
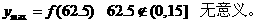
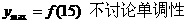
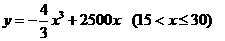
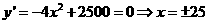
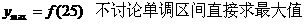
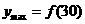
 则方程
则方程 有实数根”的逆命题
有实数根”的逆命题 有根,则
有根,则 ”,或“若方程
”,或“若方程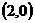 ,则此双曲线的方程是
.
,则此双曲线的方程是
.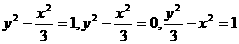 ,
,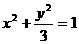 ”.
”.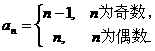
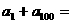 ,
, .
. 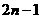 ,
,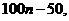 5050等.
5050等.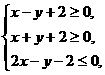 所确定的平面区域记为
所确定的平面区域记为 是区域
是区域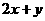 的最大值是
; 若圆
的最大值是
; 若圆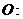
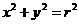 上的所有点都在区域
上的所有点都在区域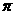 ”.
”. .
.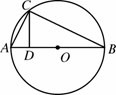
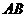 上的射影为
上的射影为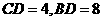 ,则圆
,则圆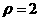 上的点到直线
上的点到直线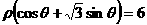
 .
.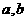 为正数,且
为正数,且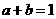 ,则
,则 的最小值是
.
的最小值是
.
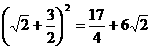 .
.

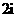 B.
-
B.
-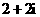 D.
D. 
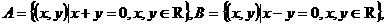 则集合
则集合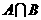 的元素个数是
的元素个数是 R, 向量
R, 向量 ,若
,若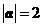 ,则
,则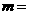
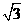 C.
C.
 D.
D.
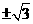
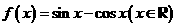 的最小正周期是
的最小正周期是 B.
B.
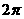 D.
D.

 4. 如图1所示,
4. 如图1所示, 是全集,
是全集,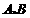 是
是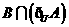
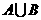 D.
D. 
 B.
B.  C.
C.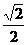 D.
D. 6(理5). 如图2所示的算法流程图中(注:“
6(理5). 如图2所示的算法流程图中(注:“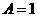 ”也可写成“
”也可写成“ ”或“
”或“ ”,均表示赋值语句),第3个输出的数是
”,均表示赋值语句),第3个输出的数是
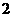 D.
D.

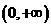 上单调递增的是
上单调递增的是
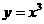 B.
B. 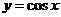
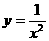 D.
D. 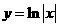
 A.
A.
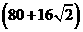 cm
cm B.
B. 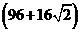 cm
cm 有3个不同的零点,
有3个不同的零点, B.
B.
 图3
图3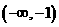 D.
D. 
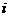 条边的边长记为
条边的边长记为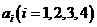 ,
,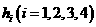 ,若
,若 ,
, 则
则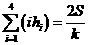 .类比以上性质,体积为
.类比以上性质,体积为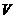 的三棱锥的第
的三棱锥的第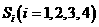 , 此三棱锥内任一点
, 此三棱锥内任一点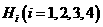 ,若
,若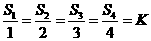 , 则
, 则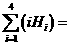
 B.
B. 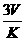 C.
C.
 D.
D.
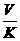 图4
图4 的大致图像才能较快的作答,理12(文13)必须准确的画出平面区域
的大致图像才能较快的作答,理12(文13)必须准确的画出平面区域 (Ⅰ)写出曲边四边形
(Ⅰ)写出曲边四边形  的面积需要用到微积分和定积分基本定理以及对图形进行合理的组合,在计算
的面积需要用到微积分和定积分基本定理以及对图形进行合理的组合,在计算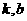 的关系式
的关系式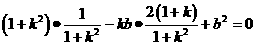 之后,若善于把变量
之后,若善于把变量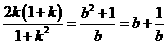 ,则可以找到运算的方向,大部分学生没有掌握.
,则可以找到运算的方向,大部分学生没有掌握.