4、已知函数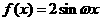 在区间
在区间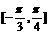 上的最小值为
上的最小值为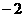 ,则
,则 的取值范围是 D
的取值范围是 D
A.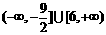 B.
B.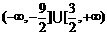
C.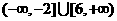 D.
D.
|
|
|
4 |
|
|
|
|
|
|
|
|
9 |
A |
3 |
5 |
|
|
|
7 |
|
2 |
|
|
6 |
|
|
3 |
5 |
|
|
|
4 |
2 |
8 |
|
6 |
9 |
|
|
|
|
1 |
|
|
|
|
|
7 |
|
|
|
|
6 |
9 |
|
3 |
5 |
4 |
|
|
|
2 |
8 |
|
|
9 |
|
B |
5 |
|
1 |
|
|
|
2 |
8 |
7 |
6 |
|
|
|
|
|
|
|
|
4 |
|
|
 若函数
若函数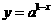
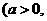 且
且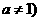 ,图象恒过定点A,又点A在直线
,图象恒过定点A,又点A在直线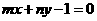 上,若
上,若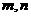 是正数,则
是正数,则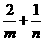 的最小值是
.
的最小值是
.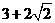
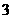 B.
B.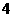 C.
C.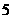 D.
D.
 在区间
在区间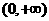 内的全部极值点按从小到大的顺序排成数列
内的全部极值点按从小到大的顺序排成数列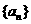 ,
,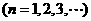 .
.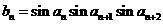 ,求证:
,求证: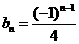 ,
,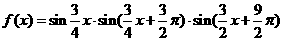
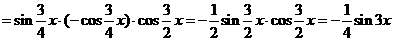
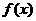 的极值点为
的极值点为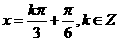 ,从而它在区间
,从而它在区间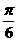 为首项,
为首项,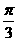 为公差的等差数列,
为公差的等差数列,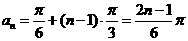 ,
,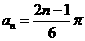 知对任意正整数
知对任意正整数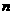 ,
,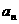 都不是
都不是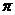 的整数倍,
的整数倍, ,从而
,从而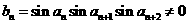
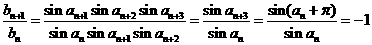
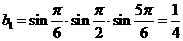 ,
,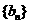 是以
是以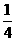 为首项,
为首项,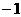 为公比的等比数列。 ∴
为公比的等比数列。 ∴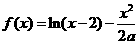 (
(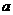 为常数且
为常数且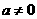 )
)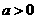 时,求
时,求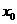 处取得极值,且
处取得极值,且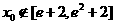 ,而
,而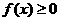 在
在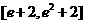 上恒成立,求实数
上恒成立,求实数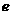 为自然对数的底数)
为自然对数的底数)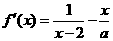 ……………………(1分)
……………………(1分)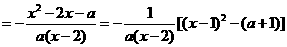
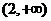 ,所以
,所以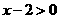
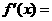
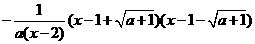
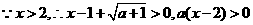
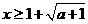 时,
时,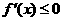 ,
,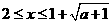 时,
时,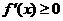 ,
,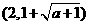
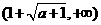 …………………(6分)
…………………(6分)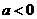 时,
时, ,
,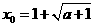
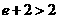 ,所以
,所以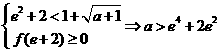 ………………………………………(9分)
………………………………………(9分)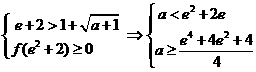 无解 ……………………(13分)
无解 ……………………(13分)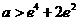 …………………………(14分)
…………………………(14分)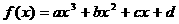 是定义在R上的函数,它在
是定义在R上的函数,它在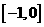 和
和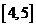 上有相同的单调性,在
上有相同的单调性,在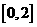 和
和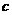 的值;
的值;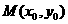 ,使得
,使得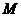 的切线斜率为
的切线斜率为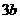 ?若存在,求出
?若存在,求出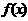 的图象交
的图象交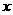 轴于
轴于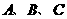 三点,且
三点,且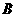 的坐标为
的坐标为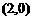 ,求线段
,求线段 的长度
的长度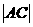 的取值范围.
的取值范围.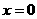 是
是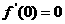 ,即
,即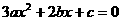 的一个解,所以
的一个解,所以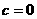 .
.
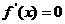 在
在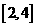 上必有一根.又
上必有一根.又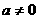 ,易知方程
,易知方程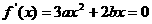 一根为
一根为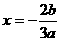 ,所以
,所以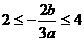 ,∴
,∴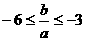
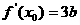 ,即
,即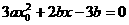 有解.而
有解.而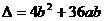 =
=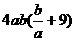 ,因为
,因为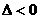 ,与
,与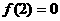 ,又
,又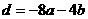 ,
,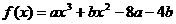 =
=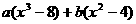
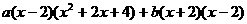 =
=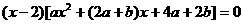 ,
,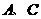 两点的横坐标
两点的横坐标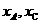 就是方程
就是方程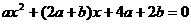 的两根,所以
的两根,所以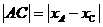 =
=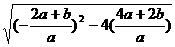 =
=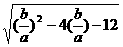 =
=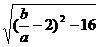 ,
, 时,
时,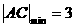 ;当
;当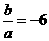 时,
时,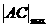 =
=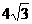 .
.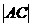 的取值范围是
的取值范围是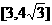 .
.
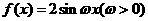 在区间
在区间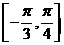 上的最小值是
上的最小值是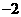 ,则
,则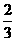 B.
B.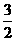 C.2 D.3
C.2 D.3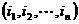 (
(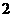 的正整数),如果在
的正整数),如果在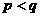 时有
时有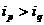 ,则称
,则称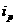 与
与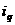 是该数组的一个“逆序”,一个数组中所有“逆序”的个数称为此数组的“逆序数”.若各数互不相等的正数数组
是该数组的一个“逆序”,一个数组中所有“逆序”的个数称为此数组的“逆序数”.若各数互不相等的正数数组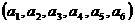 的“逆序数”是2,则
的“逆序数”是2,则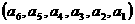 的“逆序数”是 .
13
的“逆序数”是 .
13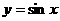 的定义域为
的定义域为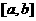 ,值域为
,值域为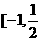 ],则
],则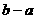 的最大值和最小值之和为B
的最大值和最小值之和为B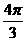 B.2
B.2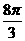 D.
D.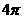
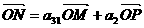 (直线MP不过点O),则S32等于 ( B )
(直线MP不过点O),则S32等于 ( B )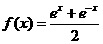 ,
, ,计算
,计算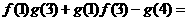 ________,
________,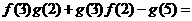 ________,并由此概括出关于函数
________,并由此概括出关于函数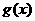 的一个等式,使上面的两个等式是你写出的等式的特例,这个等式是_______________
的一个等式,使上面的两个等式是你写出的等式的特例,这个等式是_______________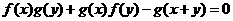
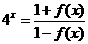 ,正实数
,正实数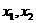 满足
满足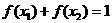 ,则
,则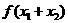 的最小值为 D
的最小值为 D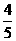
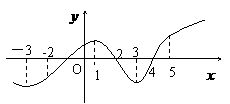 如图,是函数
如图,是函数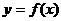 的导函数
的导函数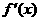 的图象,则下面判断正确的是 C
的图象,则下面判断正确的是 C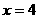 时,
时,