摘要:若函数且.图象恒过定点A.又点A在直线上.若是正数.则的最小值是 . 要在边长为16米的正方形草坪上安装喷水龙头.使整个草坪都能喷洒到水.假设每个喷水龙头的喷洒范围都是半径为6米的圆面.则需安装这种喷水龙头的个数最少是 ( B) A. B. C. D. 将函数在区间内的全部极值点按从小到大的顺序排成数列.. (Ⅰ)求数列的通项公式, (Ⅱ)设.求证:.. 解:(Ⅰ)∵ ∴的极值点为.从而它在区间内的全部极值点按从小到大排列构成以为首项.为公差的等差数列. ∴. (Ⅱ)由 知对任意正整数.都不是的整数倍. 所以.从而 于是 又. 是以为首项.为公比的等比数列. ∴. 已知函数(为常数且) (1)当时.求的单调区间 (2)若在处取得极值.且.而在上恒成立.求实数的取值范围(其中为自然对数的底数) 解:(1)由得-------- 又的定义域为.所以 当时. 当时..为减函数 当时..为增函数--------- 所以当时.的单调递增区间为 单调递减区间为------- 知当时..递增无极值--- 所以在处有极值.故且 因为且.所以在上单调 当为增区间时.恒成立.则有 --------------- 当为减区间时.恒成立.则有 无解 -------- 由上讨论得实数的取值范围为 ---------- 已知是定义在R上的函数.它在和上有相同的单调性.在和上有相反的单调性. (Ⅰ)求的值, (Ⅱ)在函数的图象上是否存在点.使得在点的切线斜率为?若存在.求出点的坐标.若不存在.则说明理由, (Ⅲ)设的图象交轴于三点.且的坐标为,求线段的长度的取值范围. 解:(Ⅰ)由题意可知在[-1.0]和[0.2]上有相反的单调性.所以是的一个极值点. 故.即是的一个解.所以. (Ⅱ)因为在 和上有相反的单调性.所以在上必有一根.又.易知方程一根为.另一根为.所以.∴ 假设存在点.使得在点的切线斜率为.则.即有解.而=.因为.所以.与有解矛盾.故不存在点.使得在点的切线斜率为. (Ⅲ)依题意有.又.所以. 所以= ==. 两点的横坐标就是方程 的两根.所以 ===. 因为.所以当时.,当时.=. 所以的取值范围是.
网址:http://m.1010jiajiao.com/timu3_id_4455950[举报]
(A类)已知函数g(x)=(a+1)x-2+1(a>0)的图象恒过定点A,且点A又在函数f(x)=log
(x+a)的图象上.
(1)求实数a的值; (2)解不等式f(x)<log
a;
(3)|g(x+2)-2|=2b有两个不等实根时,求b的取值范围.
(B类)设f(x)是定义在R上的函数,对任意x,y∈R,恒有f(x+y)=f(x)+f(y)
(1)求f(0)的值; (2)求证:f(x)为奇函数;
(3)若函数f(x)是R上的增函数,已知f(1)=1,且f(2a)>f(a-1)+2,求a的取值范围.
查看习题详情和答案>>
| 3 |
(1)求实数a的值; (2)解不等式f(x)<log
| 3 |
(3)|g(x+2)-2|=2b有两个不等实根时,求b的取值范围.
(B类)设f(x)是定义在R上的函数,对任意x,y∈R,恒有f(x+y)=f(x)+f(y)
(1)求f(0)的值; (2)求证:f(x)为奇函数;
(3)若函数f(x)是R上的增函数,已知f(1)=1,且f(2a)>f(a-1)+2,求a的取值范围.
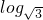 (x+a)的图象上.
(x+a)的图象上.