摘要:21.设函数=-0<<1. (1)求函数的单调区间.极值. (2)若当时.恒有≤.试确定的取值范围. [解]:(1). 令得x=a或x=3a 由表 () α () 3α () - 0 + 0 - 递减 递增 b 递减 可知:当时.函数f ()为减函数.当时.函数f()也为减函数:当时.函数f()为增函数. (2)由≤.得-≤-≤.∵0<<1. ∴+1>2. =-在[+1.+2]上为减函数.∴[]max =′(+1)=2-1, []min=′(+2)=4-4.于是.问题转化为求不等式组的解. 解不等式组.得≤≤1.又0<<1. ∴所求的取值范围是≤≤1.
网址:http://m.1010jiajiao.com/timu3_id_4455030[举报]

 的表达式;
的表达式; 的单调区间、极大值、极小值。
的单调区间、极大值、极小值。 .
. 的单调区间;
的单调区间; 的取值范围;
的取值范围;
 的表达式;
的表达式; 的单调区间、极大值、极小值。
的单调区间、极大值、极小值。 sin2x+m).
sin2x+m). 时,-4<f(x)<4恒成立,求实数m的取值范围.
时,-4<f(x)<4恒成立,求实数m的取值范围. .
. 的奇偶性;
的奇偶性; 上增减性,并进行证明;
上增减性,并进行证明; 时,不等式
时,不等式 恒成立,求实数
恒成立,求实数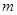 的取值范围.
的取值范围.